Domain Constrained Advertising Keyword Generation

ABSTRACT

Advertising (ad for short) keyword suggestion is important for sponsored search to improve online advertising and increase search revenue. There are two common challenges in this task. First, the keyword bidding problem: hot ad keywords are very expensive for most of the advertisers because more advertisers are bidding on more popular keywords, while unpopular keywords are difficult to discover. As a result, most ads have few chances to be presented to the users. Second, the inefficient ad impression issue: a large proportion of search queries, which are unpopular yet relevant to many ad keywords, have no ads presented on their search result pages. Existing retrieval-based or matching-based methods either deteriorate the bidding competition or are unable to suggest novel keywords to cover more queries, which leads to inefficient ad impressions.

To address the above issues, this work investigates to use generative neural networks for keyword generation in sponsored search. Given a purchased keyword (a word sequence) as input, our model can generate a set of keywords that are not only relevant to the input but also satisfy the domain constraint which enforces that the domain category of a generated keyword is as expected. Furthermore, a reinforcement learning algorithm is proposed to adaptively utilize domain-specific information in keyword generation. Offline evaluation shows that the proposed model can generate keywords that are diverse, novel, relevant to the source keyword, and accordant with the domain constraint. Online evaluation shows that generative models can improve coverage (COV), click-through rate (CTR), and revenue per mille (RPM) substantially in sponsored search.

KEYWORDS

ad keyword generation, domain constraint, reinforcement learning, Information systems → Sponsored search advertising; Query log analysis; Query suggestion

INTRODUCTION

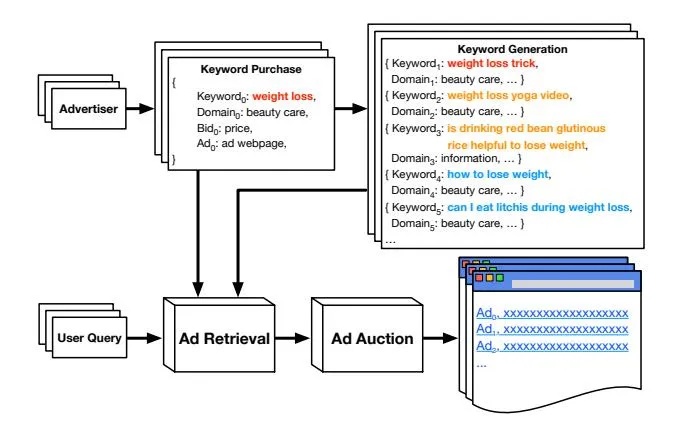
Figure 1: The sponsored search with keywords generated by our model. The red/orange/blue keywords are the keywords which have more than 3/less than 3/no ads on the impression webpage respectively.

Advertising (ad for short) keyword suggestion is an important task for sponsored search which is one of the major types of online advertising and the major source of revenue for search companies. In sponsored search, a search engine first retrieves a set of advertisements whose keywords match a user issued query. It then ranks these advertising candidates according to an auction process by considering both the ad quality and the bid price of each ad [3]. Finally, the chosen advertisement is presented in a search result page. Therefore, ad keywords are vital for ads to gain access to the auction process and have the chance to be displayed on a search result page.

However, there are two common challenges that should be addressed in sponsored search. The first one is the keyword bidding problem: due to the Matthew effect [29], the hot ad keywords become too expensive for most of the advertisers, because too many advertisers bid on such keywords. As a result, many advertisers cannot survive in the auction process to get their desired ad impressions. As reported in [43], 55.3% advertisers have no ad impression, and 92.3% advertisers have no ad click at all, which is mainly caused by low bid price or improper keywords that they bid. The second issue is inefficient ad impressions: a substantial proportion of search queries, which are unpopular yet relevant to many ad keywords, have less competitive ads (46.6% search queries) even no ads (41.0% search queries) on their search result pages as reported in [43]. Because of the two reasons, the expectation of advertisers is not satisfied and the revenue of search engines is also not optimized.

To address these problems, several prior studies have been conducted in keyword generation or suggestion [2, 8, 13, 23, 30]. Most of these studies adopt matching methods based on the word cooccurrence between ad keywords [8] and queries [13]. However, these methods tend to suggest popular keywords to advertisers, which will deteriorate the bidding competition. In addition, these approaches cannot suggest novel ad keywords which do not appear in the corpus.

Recently, deep learning technologies have been applied in many natural language tasks, such as machine translation [39], ad keyword suggestion [15], and query rewriting [18]. However, it’s not trivial to adapt these neural networks to the ad keyword generation task, due to two major challenges. First, the generated ad keywords should be diversified and relevant to the original keywords to cover more user queries, which is not supported by existing neural models applied in keyword and query generation tasks. Second, the generated ad keywords should satisfy many constraints in sponsored search. For instance, to provide relevant yet unexplored ads for users, it is necessary to satisfy the domain constraint which means that the generated keywords should belong to the domain of the source keyword or several appropriate domains. For instance, a keyword in the health care domain should only match the keywords from the same domain to ensure the ad quality, while a keyword from the information domain could match those from various domains, such as entertainment and shopping, to cover diverse user queries.

In this paper, we investigate to use generative neural networks in the task of ad keyword generation. Given the purchased keyword as input, our generative model can suggest a set of keywords based on the semantics of the input keyword, as shown in Figure 1. The generated keywords are diverse and even completely novel (the blue keywords) from those in the dataset. This generative approach can address the aforementioned problems in two ways. First, our model is able to generate diverse, novel keywords, instead of merely suggesting the existing popular keywords in the dataset, which can recommend keywords for advertisers to alleviate the keyword bidding problem and retrieve ads by keyword reformulation for sponsored search engines to address the inefficient ad impression issue. Second, to improve the quality of the generated keywords, we incorporate the domain constraint in our model, which is a key factor considered in sponsored search to display ads. Through capturing the domain constraint, our model learns both semantic information and domain-specific information of ad keywords during training, and is consequently able to predict the proper domain category and generate the ad keyword based on the predicted category. In addition, our model uses reinforcement learning to strengthen the domain constraint in the generation process, which further improve the domain correlation and the keyword quality.

To summarize, this paper makes the following contributions:

• This work investigates to use generative neural networks for keyword generation in sponsored search, which addresses the issues of keyword bidding and inefficient ad impressions.
• We present a novel model that incorporates the domain constraint in ad keyword generation. The model is able to predict a suitable domain category and generate an ad keyword correspondingly. A reinforcement learning algorithm is devised to adaptively utilize domain-specific information in keyword generation, which further improves the domain consistency and the keyword quality.
• We perform offline and online evaluation with the proposed model, and extensive results demonstrate that our model can generate diverse, novel, relevant, and domain-consistent keywords, and also improves the performance of sponsored search.

2 RELATED WORK

2.1 Keyword Generation

A variety of methods has been proposed for generating and suggesting the keywords for advertisements, as ad keywords play a critical role in sponsored search. Joshi and Motwani [23] collected text-snippets from search engine given the keyword as input, and constructed them as a graph model to generate relevant keywords based on the similarity score. Abhishek and Hosanagar [2] further improved the graph model, which computes the similarity score based on the retrieved documents. Chen et al. [8] applied concept hierarchy to keyword generation, which suggests new keywords according to the concept information rather than the co-occurrence of the keywords itself. Fuxman et al. [13] made use of the queryclick graph to compute the keyword similarity for recommendation based on a random walk with absorbing states. Ravi et al. [32] introduced a generative approach, a monolingual statistical translation model, to generate bid phrases given the landing page, which performs significantly better than extraction-based methods. Recently due to the advances of deep learning, various neural network models have been applied to ad keyword suggestion. Grbovic et al. [15] proposed several neural language models to learn low-dimensional, distributed representations of search queries based on context and content of the ad queries within a search session. Zhai et al. [41] applied an attention network which is stacked on top of a recurrent neural network (RNN) and learns to assign attention scores to words within a sequence (either a query or an ad).

2.2 Query Generation

Another related research topic is query generation, which is widely studied and applied in organic search. It improves user experience by either expanding (reformulating) a user’s query to improve retrieval performance, or providing suggestions through guessing the user intention, according to the user’s behaviour pattern (query suggestion). Some previous studies adopt query logs to generate queries by handcrafted features such as click-through data [11, 25, 35, 42], session based co-occurrence [17, 20, 22] or query similarity [4, 6, 12]. Recently, artificial neural networks have been applied in query processing. A hierarchical recurrent encoder-decoder model [38] is introduced to query suggestion. He et al. [18] proposed a learning to rewrite framework consisting of a candidate generating phase and a candidate ranking phase for query rewriting. Song et al. [37] use an RNN encoder-decoder to translate a natural language query into a keyword query. An attention based hierarchical neural query suggestion model that combines a session-level neural network and a user-level neural network to model the short- and long-term search history of a user is proposed by Chen et al. [7]

2.3 Generative Neural Network

Recently, generative neural networks have been applied in many natural language tasks, such as machine translation [39], dialogue generation [34], and query rewriting [18]. Sutskever et al. [39] apply an end-to-end approach, a sequence to sequence (Seq2Seq) model, on machine translation tasks. Shang et al. [34] further introduce the Seq2Seq model to dialogue generation tasks with novel attention mechanisms. Although the Seq2Seq model is capable of generating a sequence with a certain meaning, it isn’t suitable for diversified sequence generation as argued in [27]. Therefore, latent variable based models are proposed to address the diversity and uncertainty problem. Serban et al. [33] introduce latent variables to a hierarchical encoder-decoder neural network to explicitly model generative processes that possess multiple levels of variability. Zhou and Wang [45] propose several conditional variational autoencoders to use emojis to control the emotion of the generated text. Zhao et al. [44] use latent variables to learn a distribution over potential conversational intents based on conditional variational autoencoders, that is able to generate diverse responses using only greedy decoders.

3 MODEL

3.1 Background: Encoder-Attention-Decoder Framework

We first introduce a general encoder-attention-decoder framework based on sequence-to-sequence (Seq2Seq) learning [39], which is a widely used generative neural network. The encoder and decoder of the Seq2Seq model [39] are implemented with GRU [9, 10].

The encoder represents an input sequence $X = x_1x_2 \cdots x_n$ with hidden representations $H = h_1h_2 \cdots h_n^{-1}$ , which is briefly defined as below:

\mathbf{h}_t = \text{GRU}(\mathbf{h}_{t-1}, \mathbf{e}(x_t)), \tag{1}

where $e(x_t)$ is the embedding of the word $x_t$ , and GRU is gated recurrent unit [9].

The decoder takes as input a context vector $c_t$ and the embedding of a previously decoded word $e(y_{t-1})$ , and updates its state $s_t$ using another GRU:

$s_t = GRU(s_{t-1}, [c_{t-1}; e(y_{t-1})]),$ (2)

where $[c_{t-1}; e(y_{t-1})]$ is the concatenation of the two vectors, serving as input to the GRU network. The context vector $c_t$ is designed to attend to the key information of the input sequence during decoding, which is a weighted sum of the encoder’s hidden states as

$c_{t-1} = \sum_{k=1}^{n} \alpha_k^{t-1} h_k$ , and $\alpha_k^{t-1}$ measures the relevance between state $s_{t-1}$ and hidden state $h_k$ . Refer to [5] for more details.

Once the state vector $s_t$ is obtained, the decoder generates a token by sampling from the generation distribution $o_t$ computed from the decoder’s state $s_t$ as follows:

$y_t \sim \mathbf{o}_t = P(y_t \mid y_1, y_2, \cdots, y_{t-1}, \mathbf{c}_t),$ (3)

= \operatorname{softmax}(\mathbf{W}_{\mathbf{o}}\mathbf{s}_t). \tag{4}

3.2 Task Definition and Overview

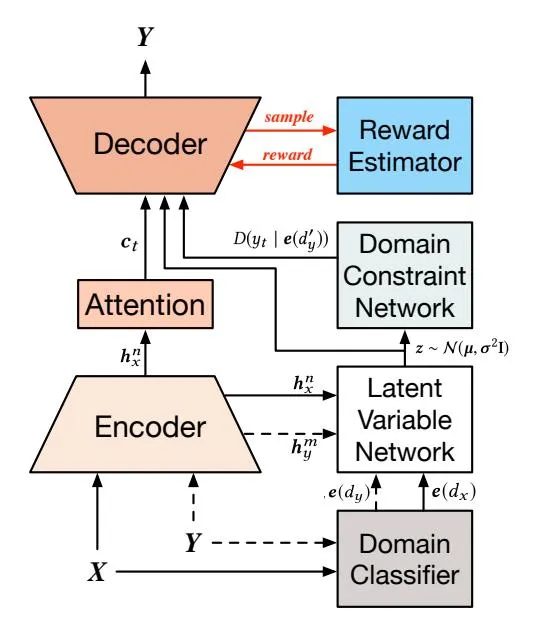
Figure 2: Overview of DCKG. The dashed arrow is used only in supervised training. The red arrow is used only in reinforcement learning. During reinforcement learning, DCKG infers a set of keyword samples and get their rewards from the reward estimator, which are used to further train our model to improve the quality of generated keywords.

Our problem is formulated as follows: Given a purchased ad keyword $X=(x_1,x_2,\cdots,x_n)$ (a word sequence)² and the corresponding domain category $d_x$ obtained from a domain classifier, the goal is to predict a suitable target domain category $d_y$ and generate a target keyword $Y=(y_1,y_2,\cdots,y_m)$ (a word sequence) that is coherent with the domain category $d_y$ . Essentially, the model estimates the probability: $P(Y,d_y|X,d_x)=P(d_y|X,d_x)\prod_{t=1}^m P(y_t|y_{<t},d_y,X,d_x)$ . The domain categories are adopted from the sponsored search engine, which consists of k domain categories, such as beauty care, shopping, and entertainment.

Building upon the encoder-attention-decoder framework, we propose the Domain-Constrained Keyword Generator (DCKG) to generate diversified keywords with domain constraints using three mechanisms. First, DCKG incorporates a latent variable sampled from a multivariate Gaussian distribution to generate diversified keywords. Second, a domain constraint network is proposed to

$^{^1{\}rm Throughout}$ the paper, a bold character (e.g., $\pmb{h})$ denotes the vector representation of a variable ( $\pmb{h}$ ).

$^{^2{\}rm Throughout}$ the paper, a keyword refers to a word sequence, but not a single word.

facilitate generating domain-consistent keywords, which imposes more probability bias to domain-specific words. Third, DCKG further optimizes the decoder to adjust the word generation distribution with reinforcement learning.

An overview of DCKG is presented in Figure 2, which illustrates the dataflow of DCKG in supervised learning, reinforcement learning, and inference processes. In supervised learning, the source keyword $X = (x_1, x_2, \dots, x_n)$ and the target keyword $Y = (y_1, y_2, \dots, y_m)$ are fed to the encoder to generate the hidden representations $\boldsymbol{h}_{x}^{n}$ and $\boldsymbol{h}_{y}^{m}$ , meanwhile, they are fed to the domain classifier to obtain their domain categories $d_x$ and $d_y$ respectively. The domain categories are further converted to the domain embeddings $e(d_x)$ and $e(d_y)$ to encode the domain-specific information in DCKG. Then, the latent variable z is sampled from a multivariate Gaussian distribution, which is determined by a recognition network that takes the hidden representations and the domain embeddings as input. Given the latent variable z, the hidden representation of source keyword $h_x^n$ , and the domain embedding $e(d_x)$ , DCKG predicts the target keyword category $d'_{u}$ and generate the domain-specific word score $D(y_t \mid e(d'_u))$ . Finally, the decoder takes as input the context vector $c_t$ generated by attention mechanism, the latent variable z, and the domain-conditioned word score $D(y_t \mid \boldsymbol{e}(d'_{\boldsymbol{y}}))$ to generate the target keyword Y.

During the inference process, DCKG has the input of only the source keyword $X = (x_1, x_2, \dots, x_n)$ to generate a target keyword, conditioned on the latent variable sampled from a prior network which is approximated by the recognition network during supervised training.

During the reinforcement learning process, DCKG first infers a set of keyword samples. Then, these samples are fed to the reward estimator to get their rewards, considering both domain-specific and semantic information. Finally, these rewards are applied to train our model using reinforcement learning to further improve the quality of generated keywords.

3.3 Supervised Learning

We will concentrate on introducing the latent variable network, the domain constraint network, and the decoder network, as shown in Figure 3. The domain classifier is adopted from the sponsored search engine with parameters fixed during training. It generates a one-hot domain category distribution $d_X$ for a keyword. A category is converted to a domain category embedding as follows:

\mathbf{e}(d_{x}) = \mathbf{V_{d}}d_{x},\tag{5}

where $\mathbf{V}_{\mathbf{d}}$ is a random initialized domain category embedding matrix which will be learned automatically.

3.3.1 Latent Variable Network. Building upon the encoder-attention-decoder framework, our model introduces a latent variable to project ad keywords to a latent space. By this means, the model can generate diversified keywords conditioned on different latent variable sampled from the latent space. Specifically, we adopt the conditional variational autoencoder (CVAE) [36] as the latent variable network, which is successfully applied in language generation tasks [44, 45].

DCKG assumes the latent variable z follows a multivariate Gaussian distribution, $z \sim \mathcal{N}(\mu, \sigma^2 \mathbf{I})$ . The latent variable network consists of a prior network and a recognition network to model the

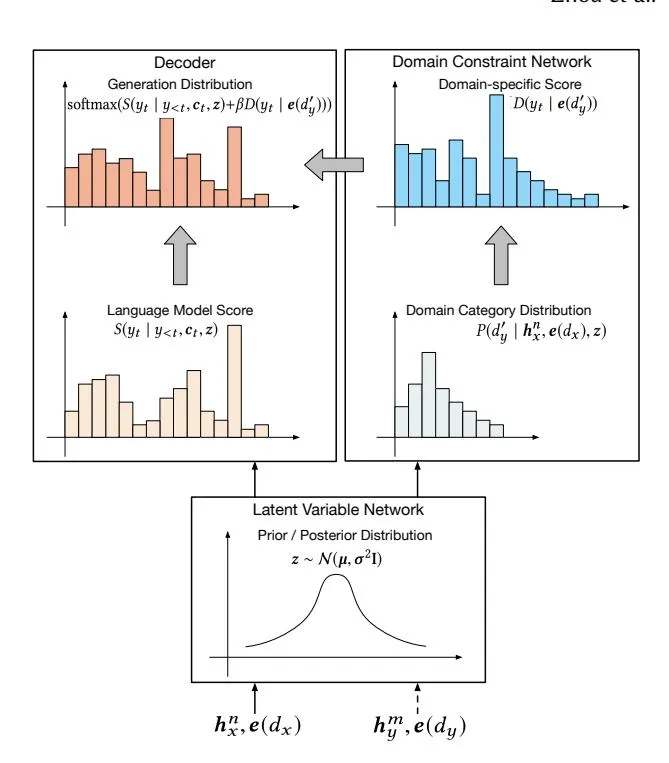
Figure 3: Computation flow of DCKG. The dashed arrow is used only in supervised learning to model the posterior distribution. During the inference process, the latent variable z is sampled from the prior distribution, and then fed to the domain constraint network and to the decoder. In the domain constraint network, the latent variable is used to predict the domain category distribution to obtain the target domain category $d_y'$ , which is then used to compute the domain-specific score. In the decoder, the latent variable is used to compute the language model score. Finally, the language model score and the domain-specific score are combined to estimate the distribution for word generation.

semantic and domain-specific information of ad keyword in the latent space.

In the training process, the recognition network takes as input the semantic representations $h_x^n, h_y^m$ and the domain embeddings $e(d_x), e(d_y)$ of the source keyword X and the target keyword Y, to approximate the true posterior distribution, as $q_{\phi}(z \mid h_x^n, e(d_x), h_y^m, e(d_y)) \sim \mathcal{N}(\mu, \sigma^2 I)$ .

In the inference process, the prior network takes only the semantic representation $h_x^n$ and the domain embedding $e(d_x)$ of the source keyword X as input, to sample latent variables from the prior distribution, $p_{\theta}(z \mid h_x^n, e(d_x)) \sim \mathcal{N}(\mu', \sigma'^2 \mathbf{I})$ . The prior/posterior distribution can be parameterized by neural networks such as a multilayer perceptron (MLP) as follows:

\left[\mu,\sigma^{2}\right] = MLP(h_{x}^{n}, e(d_{x}), h_{y}^{m}, e(d_{y})), \tag{6}

\left[\mu', \sigma'^{2}\right] = MLP(h_{x}^{n}, e(d_{x})), \tag{7}

To alleviate the inconsistency between the prior distribution and the posterior distribution, we add the KL divergence term to the loss function as follows:

$\mathcal{L}_1 = KL(q_{\phi}(z \mid \boldsymbol{h}_x^n, \boldsymbol{e}(d_x), \boldsymbol{h}_y^m, \boldsymbol{e}(d_y)) \parallel p_{\theta}(z \mid \boldsymbol{h}_x^n, \boldsymbol{e}(d_x)))$ (8)

3.3.2 Domain Constraint Network. The domain constraint network is designed to model the domain-specific information of ad keyword. The output of the network is further incorporated into the process of keyword generation to improve the quality of generated keywords in sponsored search. It plays two roles in our model: first, predicting an appropriate domain category given a latent variable; second, endowing the generated keyword with the target domain features.

Essentially, it predicts a domain category distribution conditioned on the latent variable sampled from a multivariate Gaussian distribution. Once the domain category distribution is determined, we can sample a target domain category by an argmax operation. However, argmax operation is non-differentiable and the training signal cannot be backpropagated. Inspired by the Gumbel-Max trick [16, 28], we adopt Gumbel-Softmax [19] as a differentiable substitute to generate a sample from the domain category distribution, which is defined as follows:

$\epsilon \sim U(0,1),$ (9)

$g = -\log(-\log(\epsilon)),$ (10)

$o_d = U_d MLP(h_x^n, e(d_x), z), (11)$

P_{real}(d'_u \mid \boldsymbol{h}_x^n, \boldsymbol{e}(d_x), z) = \operatorname{softmax}(\boldsymbol{o}_d), \tag{12}

$P_{sample}(d'_u \mid \boldsymbol{h}_x^n, \boldsymbol{e}(d_x), z) = \operatorname{softmax}((\boldsymbol{o}_d + \boldsymbol{g})/\tau)$ (13)

where $\epsilon$ is a sample from the uniform distribution $\mathrm{U}(0,1)$ , g is a sample from the Gumbel distribution $\mathrm{Gumbel}(0,1)$ , $o_d$ is the logits computed by a MLP and a projection matrix $\mathrm{U_d} \in \mathbb{R}^{k \times n}$ ; $P_{real}(d_y' \mid h_x^n, e(d_x), z)$ is the real distribution of the predicted domain category used in the inference process, $P_{sample}(d_y' \mid h_x^n, e(d_x), z)$ is the sample distribution used in the training process, and $\tau$ is a temperature used to adjust the shape of the sample distribution, which is annealed during training.

In supervised learning, we use the ground-truth domain category $d_y$ of a keyword as the supervision signal in the loss function, such that the domain constraint network can predict the target domain category as expected, which is defined as follows:

$\mathcal{L}_{2} = -\mathbf{E}_{q_{\phi}(\boldsymbol{z} \mid \boldsymbol{h}_{x}^{n}, \boldsymbol{e}(d_{x}), \boldsymbol{h}_{y}^{m}, \boldsymbol{e}(d_{y})}[\log P_{real}(d_{y}' \mid \boldsymbol{h}_{x}^{n}, \boldsymbol{e}(d_{x}), \boldsymbol{z})] \quad (14)$

Another task of the domain constraint network is to compute the domain-specific score of a generated word from the domain category distribution. The domain-specific score is added to the word generation distribution in the decoder to endow a generated keyword with desirable domain-specific features. When the target domain category distribution is obtained, the target domain embedding can be computed as follows:

\boldsymbol{e}(d_{u}') = \mathbf{V_d} P(d_{u}' \mid \boldsymbol{h}_{x}^{n}, \boldsymbol{e}(d_{x}), \boldsymbol{z}), \tag{15}

where $V_d$ is the domain category embedding matrix as introduced in Eq. 5. Subsequently, taking the target domain embedding as input, the domain word score is generated as follows:

D(y_t \mid \boldsymbol{e}(d'_u)) = \mathbf{W_d} \, \mathbf{MLP}(\boldsymbol{e}(d'_u)), \tag{16}

where $D(y_t \mid \boldsymbol{e}(d_y'))$ is the domain-specific score of a generated word, which models the domain-specific features of a target keyword, $\mathbf{W_d}$ is the domain word embedding matrix.

3.3.3 Decoder Network. The decoder of DCKG incorporates the latent variable and the domain word score to generate an ad keyword. Taking as input the latent variable z and the context vector $c_t$ , the language model score of a generated word, which captures the semantic information in a keyword, is generated as follows:

$s_t = GRU(s_{t-1}, [c_{t-1}; z; e(y_{t-1})]), (17)$

S(y_t \mid y_{\leq t}, c_t, z) = \mathbf{W}_{\mathbf{s}} \mathbf{s}_t, \tag{18}

where $S(y_t \mid y_{< t}, c_t, z)$ is the language model score and $\mathbf{W_s}$ is the semantic word embedding matrix.

Finally, the decoder combines the language model score and the domain-specific score with a factor $\beta$ and then normalizes the result to the word generation distribution, which is defined as follows:

P(y_t \mid y_{< t}, c_t, z, \boldsymbol{e}(d_y')) = \operatorname{softmax}(S(y_t | y_{< t}, c_t, z) + \beta D(y_t | \boldsymbol{e}(d_y'))), \tag{19}

where $\beta$ is a domain constraint factor that controls the influence of the domain-specific information in the final word generation distribution, and is fixed to 1.0 during supervised training. The generation loss of the decoder is given as below:

$\mathcal{L}_{3} = -\mathbf{E}_{q_{\phi}(\boldsymbol{z} \mid \boldsymbol{h}_{x}^{n}, \boldsymbol{e}(d_{x}), \boldsymbol{h}_{y}^{m}, \boldsymbol{e}(d_{y})} [\sum_{t=1}^{m} \log P(y_{t} \mid y_{< t}, \boldsymbol{c}_{t}, \boldsymbol{z}, \boldsymbol{e}(d_{y}'))].$

$(20)$

3.3.4 Loss Function. The final loss to be minimized in supervised learning is the combination of the KL divergence term $\mathcal{L}_1$ , the domain prediction loss $\mathcal{L}_2$ , and the generation loss $\mathcal{L}_3$ :

\mathcal{L} = \max(\delta, \mathcal{L}_1) + \mathcal{L}_2 + \mathcal{L}_3,\tag{21}

where the max operation and the factor $\delta$ are used to balance the KL divergence term and other loss function for better optimization, which is known as the free bits method in [24].

3.4 Reinforcement Learning

One major disadvantage of DCKG described above is the domain constraint factor $\beta$ is fixed for all the keywords in any domain. However, the optimal factor should be determined by the semantic and domain-specific information of a keyword dynamically. A lower $\beta$ value leads to keywords containing less domain-specific features, while a higher value results in keywords that are less fluent or relevant but contain more domain-specific features, as shown in Section 4.4. Therefore, we propose a reinforcement learning algorithm that is able to learn different $\beta$ values for different keywords.

3.4.1 Policy Network. To explore suitable $\beta$ values for different keywords, we first define a value space $\mathcal B$ which contains feasible $\beta$ values. The main idea is to choose the best $\beta$ value by a policy network to achieve the maximum reward with respect to the evaluation metrics, which can be implemented in three steps: first, generate a set of keywords with different $\beta$ values sampled from $\mathcal B$ , given the same source keyword and latent variable; second, obtain the reward of each keyword using the reward estimator; third, update the policy network to choose the $\beta$ value that leads to a maximum reward. The policy network $\pi_{\psi}(\beta \mid X, z)$ , parameterized by $\psi$ , is

formally given below:

o_b = [h_x^n; e(d_x); z; e(d_y')], \tag{22}

$\pi_{\psi}(\beta \mid X, z) = \operatorname{softmax}(\mathbf{W_b} \operatorname{MLP}(o_b)),$ (23)

where $\mathbf{W_b} \in \mathbb{R}^{b \times n}$ is a matrix projecting the input vector $\mathbf{o}_b$ to the action space $\mathcal{B}$ .

We use the REINFORCE algorithm [40], a policy gradient method, to optimize the parameters by maximizing the expected reward of a generated keyword as follows:

\mathcal{J}(\psi) = \mathbb{E}_{\beta \sim \pi_{\psi}(\beta|X,z)}[R(X,z,\beta)],\tag{24}

where $R(X, z, \beta)$ is the normalized reward of a generated keyword. It is noteworthy that the policy network cannot be optimized through supervised learning, as the ground-truth $\beta$ value is not observable.

3.4.2 Reward Estimator. The reward estimator is designed to provide a reward balancing the domain-specific information and the semantic information for a generated keyword. To estimate the reward, given the source keyword X, the latent variable z, and the target domain category $d'_y$ as the same input, we first sample a set of $\beta$ values $\{\beta_1, \beta_2, \dots, \beta_k\}$ , and infer a set of keyword samples $\{Y_1, Y_2, \cdots, Y_k\}$ based on different $\beta$ samples using the proposed model. Then, we use the domain classifier to predict the domain category $d_{y_i}$ of each keyword $Y_i$ . The agreement $\gamma$ between $d'_u$ and $d_{u_i}$ is treated as an evaluation metric of the domain-specific information, which is defined as follows:

undefined