Dynamic Reserve Price Design With Distributed Solving Algorithm

ABSTRACT

Unexpected advertising items in sponsored search may reduce users’ reliance on organic search, resulting in hidden cost for the e-commerce platform. To address this problem and promote sustainable growth, we propose a dynamic reserve price design that incorporates the hidden cost into the auction mechanism to determine whether to sell the traffic, thereby ensuring a balanced relationship between revenue and user experience. Our dynamic reserve price design framework optimizes traffic sales by minimizing impacts on user experience while maintaining long-term incentives for advertisers to reveal their valuations truthfully. Furthermore, we introduce a distributed algorithm capable of computing reserve prices with billion-scale data in the production environment. Experiments involving offline evaluations and online A/B testing demonstrate that this method is simple and efficient, making it suitable for use in industrial production. This method has already been fully deployed in the production environment.

KEYWORDS

reserve price, large-scale distributed algorithm, sponsored search, advertising, Information systems → Computational advertising.

1 INTRODUCTION

Advertising plays an important role in Internet companies such as Google and Meta, and it is also the most efficient strategy of monetization in e-commerce platforms such as Amazon and Alibaba. To create a sustainable growth flywheel for e-commerce platforms, it’s important to establish a closed-loop among monetization, user growth and platform Gross Merchandise Volume (GMV). When revenue generated from ads is invested into user growth, new or retained users increase the platform’s value to sellers. However, it is commonly agreed that search ads will hurt user experience and GMV. The main reason is the different objective set by the ad and the organic search. The former aims to optimize cost per mille (CPM), while the latter focuses on maximizing Gross Merchandise Volume per mille (GPM). Therefore, establishing a relationship between user experience and revenue when filling ads is both necessary and important. Auction mechanisms, such as reserve price design, can be used to achieve these goals.

Typically, the conversion rate (CVR) or click-through rate (CTR) threshold is used to determine whether to sell the traffic, but it will impose a negative impact on advertisers especially when they are introducing new products due to the uncertainty of estimation. Under this mechanism, no matter how much advertisers raise their bid price, they will not get the traffic and may ultimately abandon the campaign. Other methods like [28] attempt to design a mechanism that encourages advertisers to create an experience for users that maximizes efficiency, but it doesn’t work well when ad supply is not sufficient for some traffic because poor quality ads with low bid price may still have the opportunity for impression. From the perspective of reserve price design, to maximize the revenue earned in a generalized second price auction (GSP) [1], the platform can set a reserve price and not make any allocations when the bids are low [22]. Lots of work has been done to find the optimal reserve price to improve platform revenue from the perspective of advertisers, and maintain incentive compatibility to prevent bid shading issues[6? –8]. A widely used method is based on advertisers’ historical behavior [10–14]. In order to estimate the traffic value, the idea is to use advertisers’ history of bids. However, there are two drawbacks of this kind of method, one is that it relies on advertisers’ original bids to calculate the reserve price, which makes us more careful about the incentive problems.

In our proposed method, we design a framework that generates dynamic reserve price to maximize the expected cost per mille (ECPM) under platform constraints. This framework establishes the relationship among revenue, user experience and monetization ratio while keeping the incentive compatible as well. To compute the reserve price on a large scale of data, we propose distributed algorithms that enable the practical implementation of this design in industrial production.

2 PRELIMINARIES

In a typical auction, advertisers compete for traffic opportunities in sponsored search scenario, where represents the traffic volume. The traffic $i, \forall i \in [N]$ , is allocated to the advertiser who has the highest ECPM. The estimated $ecpm_i$ for each traffic signifies the potential revenue, calculated in the Cost Per Click (CPC) model as $ecpm_i = ctr_ibid_i$ . Here, $bid_i$ and $ctr_i$ are bid price and the estimated CTR of the winning advertiser for traffic i, respectively.

2.1 Problem Formulation

As discussed in section 1, it is essential to understand the relationship among revenue, user experience and monetization ratio. To this end, platform constraints have been defined as equations (2)-(4). We discuss the reserve price mechanism design without considering estimation uncertainty and model the problem as an optimization problem, such that

\max_{x_i} \sum_{i=1}^{N} ecpm_i x_i \tag{1}

s.t. $\sum_{i=1}^{N} (ctr_i - tctr) x_i \ge 0$ (2)

\sum_{i=1}^{N} (gpm_i - tgpm) x_i \ge 0 \tag{3}

\sum_{i=1}^{N} -x_i \ge -tpv \tag{4}

$x_i \in \{0, 1\}, \forall i \in [N].$ (5)

The total revenue is expressed as $\sum_{i=1}^{N} ecpm_i x_i$ , where $x_i$ is the decision variable indicating whether the traffic is sold $(x_i=1)$ or reserved $(x_i=0)$ . Here, $ecpm_i$ is the ECPM for traffic i, and tctr, tgpm represent the largest lower bound of CTR and GPM, respectively. The two constants, set by the platform, define user experience boundaries. Additionally, tpv represents the smallest upper bound of ads impressions, used to control the monetization ratio defined as tpv/N. $ctr_i$ and $gpm_i$ are the estimated CTR and GPM for traffic i respectively.

2.2 Lagrangian Duality

In this section, we present the reserve price design framework along with its derivation. We reformulate the problem described in section 2.1 in a more generalized form

\max_{x_i} \sum_{i=1}^{N} c_i x_i \tag{6}

s.t. $\sum_{i=1}^{N} b_{ik} x_i \ge B_k, \forall k \in [K]$ (7)

$x_i \in \{0, 1\}, \forall i \in [N].$ (8)

Where K indicates the size of the constraint set, which typically remains below 10 in practical scenarios. $c_i$ and $b_{ik}$ are the coefficients of the objective and constraint, respectively, and $B_k$ denotes the largest lower bound of constraint k. $x_i$ is the binary decision variable. Using the Lagrangian decomposition [16], we have the dual problem of (6)-(8) with the Lagrange multipliers $\lambda_k$ corresponding to the inequality constraints of (7), where $\lambda_k$ is restricted to be

non-negative.

\max_{x_i} \sum_{i=1}^{N} \left( c_i + \sum_{k=1}^{K} \lambda_k b_{ik} \right) x_i - \sum_{k=1}^{K} \lambda_k B_k \tag{9}

s.t. $\lambda_k \ge 0, \forall k \in [K]$ (10)

$x_i \in \{0, 1\}, \forall i \in [N],$ (11)

based on the KKT condition [18], to maximize the problem in (9) with optimal $\lambda_k$ , we should set $x_i$ to 1 if the corresponding adjusted cost is positive. This can be interpreted as

$x_i = \begin{cases} 1, & \text{if } c_i + \sum_{k=1}^K \lambda_k b_{ik} > 0\\ 0, & \text{otherwise} \end{cases}$ (12)

Therefore, bringing the problem defined in section 2.1 into equation (12), the dynamic reserve price $r_i$ for each traffic i can be interpreted as follows

$r_i = \frac{\lambda_1 \left( tctr - ctr_i \right) + \lambda_2 \left( tgpm - gpm_i \right) + \lambda_3}{ctr_i}, \forall i \in [N]. \quad (13)$

In this context, $\lambda_1$ , $\lambda_2$ and $\lambda_3$ are the Lagrangian multipliers ¹ corresponding to constraints (2)-(4) respectively. Traffic is sold when $bid_i > r_i$ , and we can see that the computation of dynamic reserve price does not rely on the advertisers’ individual bids. Hence, the bids do not affect their utility in future auctions and myopically maximizing utility in each auction is optimal for maximizing their long-term utility.

In general, the Lagrangian techniques cannot guarantee to get an optimal solution to the primal integer programming (IP) problem, because a duality gap occurs due to the LP relaxation [27]. However, the solution computed from (9)-(11) is optimal for any IP problems derived from KKT condition when $B_k$ is replaced by $B_k-\delta_k$ [16], where $\delta_k$ is non-negative variables, which satisfy with any $\lambda_k>0$ such that $\delta_k$ is 0. But we still can use duality gap [29] to measure the optimality of the solution.

2.3 Distributed Algorithm for Dynamic Reserve

In industrial production, traffic volume is substantial. Consequently, the problem we aim to address requires solutions that leverage distributed clusters instead of a single machine. In this section, we introduce the distributed algorithm.

2.3.1 Dual Descent Dynamic Reserve Price (D3RP). First, we consider the dual descent algorithm [21]. This algorithm allows us to obtain optimal Lagrangian multipliers through the iterative procedure based on the decomposability of dual. Once $x_i$ is computed using equation (12), the Lagrangian multipliers can be updated as follows

\lambda_k^{(t)} = \max\left(\lambda_k^{(t-1)} - \alpha \left(\sum_{i=1}^N b_{ik} x_i - B_k\right), 0\right),\tag{14}

where $\alpha$ is the learning rate for each iteration, and it is sensitive since its selection may depend on the scale of the problem $t \in \{0, 1, ..., T\}$ denotes the iteration step, where T represents the maximum number of iterations. In algorithm 1, we introduce a

$^{^1\}lambda$ can be interpreted as the shadow price or marginal utility of the metrics we want to control.

distributed implementation to compute the dynamic reserve price. Particularly, in each iteration, 1) We use the map operation in Spark [?] to compute $x_i$ independently for each traffic, and then we obtain coefficients $b_{ik}x_i$ for each Lagrangian multiplier. 2) We use reduce operation to aggregate all coefficients and then collect them to the driver to update $\lambda_k$ using dual descent method as described in equation (14).

Algorithm 1 Dual Descent Dynamic Reserve Price (D3RP)

1: Initialize \lambda_k^0 = 0, \forall k \in [K]
2: repeat
3: solve x_i^{(t)}, \forall i \in [N] with multiplier \lambda_k^{(t-1)} by (12)
4: for each k \in [K] in parallel do
5: compute \sum_{i=1}^{N} b_{ik} x_i^{(t)} in parallel
6: update \lambda_k^{(t)} using (14)
7: end for
8: until \lambda_k^{(t)} has converged

2.3.2 Coordinate Descent Dynamic Reserve Price (CD2RP). The algorithm described above requires manual setting of the learning rate $\alpha$ , which can lead to a waste of computational resources when multiple hyperparameter settings are tested in data-intensive scenarios. So we propose a method using coordinate descent algorithm [20] to compute the reserve price. This approach begins by preparing the ordered collection $\Lambda_{k'}$ , as defined in (18), and then updates one coordinate $\lambda_{k'}$ using the smallest value in $\Lambda_{k'}$ that ensures the primal problem remains feasible, while keeping the other multipliers fixed. We reformulate the subproblem and present it as a coordinated update in the following form

\max_{x_i} \sum_{i=1}^{N} \left( c_i + \lambda_{k'} b_{ik'} + \sum_{k=1, k \neq k'}^{K} \lambda_k b_{ik} \right) x_i \tag{15}

s.t. $x_i \in \{0, 1\}, \forall i \in [N]$ (16)

\lambda_k \ge 0, \forall k \in [K]. \tag{17}

Let $f_i(\lambda_{k'}) = c_i + \sum_{k=1, k \neq k'}^K \lambda_k b_{ik} + \lambda_{k'} b_{ik'}, \forall i \in [N]$ . According to equation (12), the decision variable is only related to the sign of the coefficient function $f_i(\lambda_{k'})$ . The interaction with the horizontal axis can cause the decision variable to change, so the candidate set $\Lambda_{k'}$ can be defined as

\Lambda_{k'} = \{ \lambda_{k'} \mid f_i(\lambda_{k'}) = 0, \, \forall i \in [N] \}. \tag{18}

We design a dual binary search (DBS) to find the optimal $\lambda_{k'}$ for each iteration efficiently if the primal problem is feasible.

More specifically, the procedure of the algorithm 2 is as follows: 1) We compute sorted candidates of $\Lambda_{k'}^{(t)}$ using equation (18) in parallel with map operation. 2) We use algorithm 3 to identify the minimum threshold that ensures the constraint is satisfied with $B_{k'}$ and then update $\lambda_{k'}^{(t)}$ .

3 EXPERIMENTAL EVALUATIONS

3.1 Optimality Testing

Due to the challenges of solving million-scale IP problems, we conduct tests using small-scale artificial data with code that has been

Algorithm 2 Coordinate Descent Dynamic Reserve Price (CD2RP)

1: Initialize \lambda_{k'}^0 = 0, \forall k' \in [K]
2: repeat
3: for each k' \in [K] do
4: compute sorted candidate set \Lambda_{k'}^{(t)} by (18) in parallel
5: search optimal \lambda_{k'}^{(t)} and x_i^{(t)}, \forall i \in [N] with candidate set \Lambda_{k'}^{(t)} and algorithm 3
6: end for
7: until \lambda_{k'}^{(t)} has converged

Algorithm 3 Dual Binary Search (DBS)

1: Input \Lambda_{k'}^{(t)} = \{\lambda_{k',0}^{(t)}, \lambda_{k',1}^{(t)}, \dots, \lambda_{k',M-1}^{(t)}\} where M = |\Lambda_{k'}^{(t)}|

2: Initialize l = 0, u = M - 1

3: while l < u do

4: p = \lfloor (l + u)/2 \rfloor

5: solve x_i^{(t)}, \forall i \in [N] with multiplier \lambda_{k',p}^{(t)} by (12) in parallel

6: compute cons_{k'}^{(t)} = \sum_{i=1}^{N} b_{ik'} x_i^{(t)} in parallel

7: if cons_{k'}^{(t)} < B_{k'} then

8: l = p + 1

9: else

10: u = p

11: end while

12: end while

13: return \lambda_{k',u}^{(t)} and x_i^{(t)}

made available on GitHub². We generate $c_i$ and the coefficients of constraint $b_{ik}$ with uniform distributions over [0,1]. To ensure a feasible solution exists, we set the constraint $B_k$ between 0 and N. We assess the optimality ratio, defined as the ratio of the objective value obtained using SCIP $^3$ [15] to that obtained using our algorithms. We compare the two proposed algorithms across varying numbers of constraints, where $1 \le K \le 20$ , and plot the average optimality ratio curve over 20 tests as K changes. The experiment results, shown in Figure 1, indicate that the optimality ratio exceeds 0.995 when N=2000, and 0.998 when N=10000. Additionally, we observe that the optimality ratio decreases as K increases. In industrial practice, K is typically small while N is large, empirically demonstrating that a near-optimal solution can be achieved.

3.2 Duality Gap on Production Data

We test the algorithm with real search scenario data to measure the optimality of the solution. Since it is difficult to find the optimal solution to million-scale problems, one approach is to calculate the duality gap G and primal objective value V. If the relative duality gap defined as G/V is sufficiently small, it indicates that near-optimal solution has been found. We test the two algorithms with one million real data points sampled from a production environment with three constraints as described in section 2.1, and for D3RP we compare the effects of two learning rate settings of

$^{^2} https://github.com/lmxiaonuo/solver.git\\$

^<sup>3SCIP is currently one of the fastest non-commercial solvers for mixed integer programming (MIP) and mixed integer nonlinear programming (MINLP)

$\alpha=2e^{-9}$ and $\alpha=1.5e^{-9}$ respectively. Figure 2 shows the curve of the relative duality gap over 15 iterations. It indicates that we have achieved a near-optimal solution, and D3RP is sensitive to the learning rate as we explained in 2.3.1 while having a slower convergence speed than CD2RP.

3.3 Production Deployment

We present the online performance of CD2RP in the Lazada sponsored search scenario, assessing both efficiency and relevance score⁴. We consider four metrics, i.e., revenue, CTR, GPM, top query⁵ relevance and mid query⁶ relevance, and conduct online A/B testing with these metrics. We set the relevance score to be at least 85% for top queries and 75% for mid queries while ensuring that the

^<sup>6Mid query is the middle 10% of search instances.

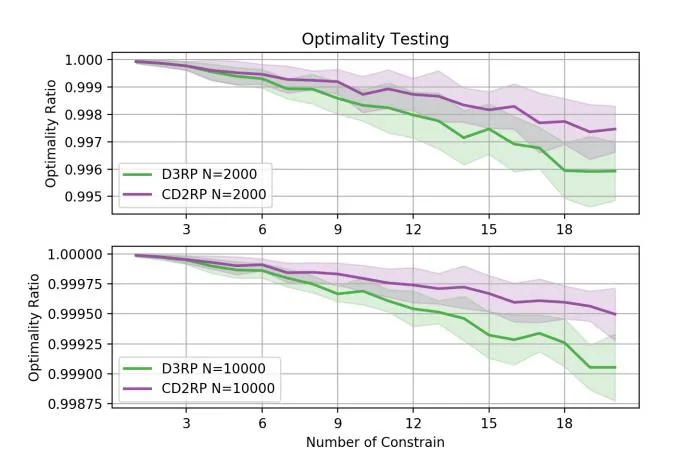
Figure 1: Optimality ratio of D3RP and CD2RP

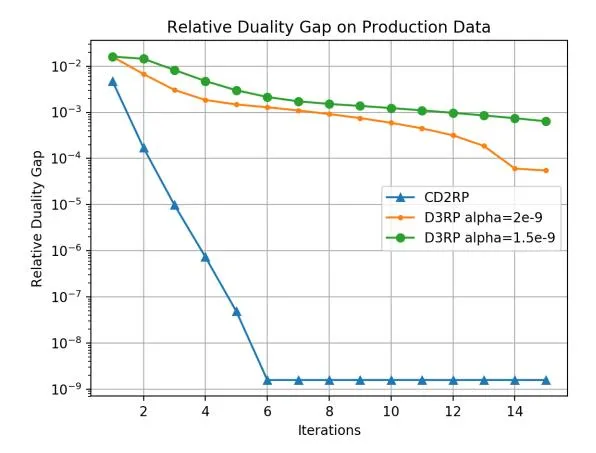
Figure 2: Duality gap curve of D3RP and CD2RP

gap in CTR and GPM between ad slots and organic search results does not exceed 20% and 30%, respectively. Table 1 shows the relative improvements seen in 10% of production traffic during a week, benchmarked against another 10% of traffic without platform constraints. It compares our method with LB-DRP [14], Opt-DRP [2], and Ada-DRP [?] under the same level of platform constraints. Our method demonstrates high performance with minimal revenue loss.

Table 1: Online experiments in Thailand

Method	CTR	GPM	Top Query Relevance	Mid Query Relevance	Revenue
LB-DRP	+18.01%	+27.09%	+57.81%	+28.46%	-5.66%
Ada-DRP	+19.46%	+27.33%	+55.45%	+26.78%	-4.31%
Opt-DRP	+21.54%	+28.09%	+58.01%	+29.13%	-3.21%
CD2RP	+23.67%	+29.54%	+58.27%	+29.62%	-1.35%

##3.4 Solving Speed

The distributed implementation of our algorithm uses Spark. We sample traffic of varying scales from real data to examine scalability. N ranges from millions to hundreds of millions with fixed K=3 (CTR, GPM and monetization ratio), setting up 512 executors, each with 1 core and 2G memory. The experiment has been tested 3 times with the same settings to get more reliable results. Figure 3 illustrates the solving time for varied scales of traffic. It indicates that CD2RP is acceptable for daily scheduling in the production environment.

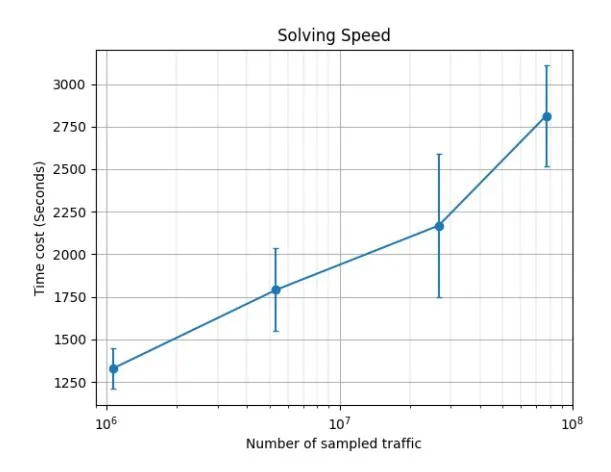
Figure 3: Time cost across different data scales using CD2RP

4 CONCLUSION

We introduce a dynamic reserve price design framework of sponsored search, which defines the relationship between revenue and user experience while maintaining incentive compatibility. We propose distributed algorithms to solve the billion-scale problem with limited constraints. The implementation provides a simple yet reliable solution for the advertising system. It has already been fully deployed in the production environment of sponsored search.

$^{^4}$ Relevance score is a human evaluation metric defining whether the ads are relevant to the query.

^<sup>5Top query is the top 50% of search instances.

REFERENCES

• [1] Myerson, R.B. Optimal auction design. Mathematics of operations research 1981, 6, 58–73.

• [2] Ostrovsky, M.; Schwarz, M. Reserve prices in internet advertising auctions: A field experiment. In Proceedings of the Proceedings of the 12th ACM conference on Electronic commerce, 2011, pp. 59–60.

• [3] Stokey, N.L. Intertemporal price discrimination. The Quarterly Journal of Economics 1979, pp. 355–371.

• [4] Salant, S.W. When is inducing self-selection suboptimal for a monopolist? The Quarterly Journal of Economics 1989, 104, 391–397.

• [5] Hart, O.D.; Tirole, J. Contract renegotiation and Coasian dynamics. The Review of Economic Studies 1988, 55, 509–540.

• [6] Villas-Boas, J.M. Price cycles in markets with customer recognition. RAND Journal of Economics 2004, pp. 486–501.

• [7] Taylor, C.R. Consumer privacy and the market for customer information. RAND Journal of Economics 2004, pp. 631–650.

• [8] Fudenberg, D.; Villas-Boas, J.M. Behavior-based price discrimination and customer recognition. Handbook on economics and information systems 2006, 1, 377–436.

• [9] Bikhchandani, S.; McCardle, K. Behavior-based price discrimination by a patient seller. The BE Journal of Theoretical Economics 2012, 12.

• [10] Amin, K.; Rostamizadeh, A.; Syed, U. Learning prices for repeated auctions with strategic buyers. Advances in Neural Information Processing Systems 2013, 26.

• [11] Acquisti, A.; Varian, H.R. Conditioning prices on purchase history. Marketing Science 2005, 24, 367–381.

• [12] Mohri, M.; Munoz, A. Optimal regret minimization in posted-price auctions with strategic buyers. Advances in Neural Information Processing Systems 2014, 27.

• [13] Chen, X.; Wang, Z. Bayesian Dynamic Learning and Pricing with Strategic Customers. 2016.

• [14] Kanoria, Y.; Nazerzadeh, H. Dynamic reserve prices for repeated auctions: Learning from bids. arXiv preprint arXiv:2002.07331 2020.

• [15] Achterberg, T. SCIP: solving constraint integer programs. Mathematical Programming Computation 2009, 1, 1–41.

• [16] Shapiro, J.F. A survey of Lagrangean techniques for discrete optimization. In Annals of Discrete Mathematics; Elsevier, 1979; Vol. 5, pp. 113–138.

• [17] Dean, J.; Ghemawat, S. MapReduce: Simplified data processing on large clusters 2004.

• [18] Boyd, S.; Boyd, S.P.; Vandenberghe, L. Convex optimization; Cambridge university press, 2004.

• [19] Agarwal, D.; Chen, B.C.; Elango, P.; Wang, X. Personalized click shaping through lagrangian duality for online recommendation. In Proceedings of the Proceedings of the 35th international ACM SIGIR conference on Research and development in information retrieval, 2012, pp. 485–494.

• [20] Wright, S.J. Coordinate descent algorithms. Mathematical Programming 2015, 151, 3–34.

• [21] Macklin, M.; Erleben, K.; Müller, M.; Chentanez, N.; Jeschke, S.; Kim, T.Y. Primal/dual descent methods for dynamics. In Proceedings of the Computer Graphics Forum. Wiley Online Library, 2020, Vol. 39, pp. 89–100.

• [22] Krishna, V. Auction theory; Academic press, 2009.

• [23] Lahaie, S.; Pennock, D.M. Revenue analysis of a family of ranking rules for keyword auctions. In Proceedings of the Proceedings of the 8th ACM Conference on Electronic Commerce, 2007, pp. 50–56.

• [24] Evans, D.S. The online advertising industry: Economics, evolution, and privacy. Journal of economic perspectives 2009, 23, 37–60.

• [25] Goldfarb, A.; Tucker, C. Online display advertising: Targeting and obtrusiveness. Marketing Science 2011, 30, 389–404.

• [26] Turban, E.; King, D.; Lee, J.K.; Liang, T.P.; Turban, D.C. Marketing and advertising in e-commerce. In Electronic commerce; Springer, 2015; pp. 403–456.

• [27] Dantzig, G.B. Discrete-variable extremum problems. Operations research 1957, 5, 266–288.

• [28] Abrams, Z.; Schwarz, M. Ad auction design and user experience. In Proceedings of the International Workshop on Web and Internet Economics. Springer, 2007, pp. 529–534.

• [29] Champion, T. Duality gap in convex programming. Mathematical programming 2004, 99, 487–498.

• [30] Aggarwal, G.; Muthukrishnan, S.; Pál, D.; Pál, M. General auction mechanism for search advertising. In Proceedings of the Proceedings of the 18th international conference on World wide web, 2009, pp. 241–250.