Efficiency Evaluation In Search Advertising

ABSTRACT

In this article, we use data envelopment analysis combined with principal component analysis to evaluate the efficiency of online retailers in search advertising. We examine various efficiency model specifications involving several resource and performancerelated variables in search advertising. Our analysis based on 200 retailers suggests different efficiency patterns for multichannel and Web-only retailers. The results of our efficiency pattern analysis indicate that the performance metrics, impressions, online sales, click-through rate, and conversion rate together reveal differences in efficiency mainly for multichannel retailers. On the other hand, ad positions in sponsored and organic links reveal differences in efficiency for Web-only retailers. In terms of overall efficiency, we find that multichannel retailers occupy relatively most of the top positions. These results contribute to organizational level understanding of search advertising practices in online retailing and offer insights into keyword management, resource utilization, and performance metrics in search advertising campaigns. [Submitted: August 17, 2011. Revised: June 22, 2012. Accepted: July 22, 2012.]

Subject Areas: B2C E-Commerce, Data Envelopment Analysis, Efficiency Analysis, Electronic Market Places, Performance Metrics and Evaluation, Principal Component Analysis, Retail Services, and Search Advertising.

INTRODUCTION

Recent advances inWeb technologies have transformed search advertising to be one of the best marketing mechanisms today. Search advertising involves the entire set of strategies and techniques advertisers use to direct visitors from search engines to their Web sites. Compared with the slow growth of traditional marketing channels, online search volumes continue to grow at a steady rate. According to the Interactive Advertising Bureau (IAB), Internet advertising revenues hit $7.3 billion in the first quarter of 2011, which is a new record and a 23% jump over the first quarter of 2010 (Wasserman, 2011). This growth can be attributed to the development of the Web as an effective marketing channel.

In addition to utilizing natural (organic) search marketing strategies, search engine advertisers compete for top ad slots provided by search brokers (e.g., Google, Yahoo!, and Microsoft Bing) through keyword auctions. This form of

*^†*Corresponding author.

online advertising, where advertisers bid for premium spots on a search engine’s results page (SERP), is commonly known as sponsored search advertising (Jansen & Mullen, 2008; Ghose & Yang, 2009). Sponsored search advertising has become the largest revenue source for search engines and the primary form of online advertising for generating leads and converting sales for advertisers (Chen, Liu, & Whinston, 2009; Ghose & Yang, 2009; Animesh, Ramachandran, & Viswanathan, 2010).

Our objective in this article is twofold. First, we analyze the competitive landscape in search advertising and provide empirical evidence on the comparative performance of firms. The sponsored search mechanism has enabled many advertisers with diverse profiles to enter the increasingly competitive keyword market. Anecdotal evidence from industry observers also suggests that most advertisers overpay for keywords in their search advertising programs. Yet despite the attention search advertising has received in academic research, little effort has been directed at rigorously examining the search advertising profiles of firms and their comparative performance in the keyword market. We believe that one effective way for firms to understand the search advertising process and improve their performance is to gain sufficient knowledge of what their competitors are doing. In other words, understanding the practices that work best in one’s competitive circle provides the foundation for search advertising strategy and a baseline to measure results against. Therefore, our study aims to provide a broader insight into the keyword market competition by analyzing the comparative performance of firms in search advertising.

Second, we attempt to provide firm-level insights into the various sponsored search metrics currently tracked by search engine providers. The search advertising process has become more dynamic and complex, due to the shift from the previous bid-only ad ranking mechanism to the current multifactor ranking mechanisms adopted by major search providers. Considering this trend, recent research on keyword auctions has also emphasized alternative mechanism designs that account for factors other than bid values (e.g., Liu & Chen, 2006; Liu, Chen, & Whinston, 2010). Consequently, advertisers need to pay attention to a variety of relevancy factors to remain competitive in the keyword market. Moreover, advertisers need to understand the relationship between different sponsored search metrics as well as the factors that drive differences in these metrics in order to effectively manage their keyword campaigns (Ghose & Yang, 2009). Because the various metrics provide different and at times conflicting assessments, evaluating and benchmarking overall search advertising performance is a non-trivial process.

In order to achieve the above research objectives, we use a methodology that combines data envelopment analysis (DEA) with principal component analysis (PCA), which is known in the literature as PCA-DEA (Ueda & Hoshiai, 1997; Adler & Berechman, 2001; Adler & Golany, 2001, 2002; Serrano-Cinca & Mar-Molinero, 2004; Adler & Yazhemsky, 2010). This methodology suits the complex setting of search advertising and allows us to explore various efficiency model specifications using multiple resource- and performance-related variables in search advertising. Although advertisers may vary in size and available resources, the current ranking mechanisms require them to perform broadly comparable activities. These include selecting relevant keywords, crafting compelling ad copies,

setting an appropriate ad budget, formulating bidding strategies, and designing search engine optimization (SEO) strategies to supplement their pay-per-click (PPC) campaigns. These activities provide the foundation for a production view of search advertising and the significance of measuring efficiency in terms of how well each firm performs when compared with its competitors.

Our empirical analyses are based on the search advertising practices of firms in online retailing, an industry characterized by extensive use of Web technologies and high-stakes battles for market share and profitability. We examine several firms which include Web-only retailers (WORs) that use the Internet as the only sales channel and multichannel retailers (MCRs) that have other sales channels in addition to the Web. Using Google-based search marketing data, we analyze their relative efficiency in search advertising. We also explore the variables that reveal differences in efficiency between MCRs and WORs. The results of our efficiency analysis suggest different patterns for MCRs and WORs. We find that the performance metrics, impressions, online sales, click-through rate (CTR), and conversion rate together reveal differences in efficiency mainly for MCRs. On the other hand, ad positions in sponsored and organic links reveal differences in efficiency for WORs. In terms of overall efficiency in search advertising, we find that MCRs occupy relatively most of the top positions.

Our research contributes to both academic literature and industry practice. For the academic community, our article offers a unique, data-driven perspective on the competitive performance of firms in sponsored search advertising based on cross-sectional data from online retailing. This contributes to a major gap in empirical research in sponsored search advertising as most of the extant research is based on field studies and experiments with a single firm’s search advertising practice. In addition, our article provides insight into conventional assumptions on the design of keyword auctions and performance-based ranking mechanisms. To the best of our knowledge, this research also represents the first application of the DEA framework to the study of efficiency in search advertising.

For advertisers, managerial decisions regarding resource allocation, performance evaluation, and benchmarking are important aspects of search advertising campaigns. Given the constant changes in the search industry, gaining measurable insights into the search advertising process will have several strategic benefits for competing firms. More importantly, advertisers need appropriate methods for performance evaluation and benchmarking that take into account the dynamics of search advertising today. Our results are based on real-life search advertising data and multiple resource- and performance-related variables that are drawn from both industry and prior literature. Therefore, these results offer important insights into keyword management, resource utilization, and performance metrics in search advertising campaigns.

For search engine providers, the study of efficiency in keyword advertising is also crucial for designing effective performance-based ranking mechanisms that could allow advertisers to pay only for measurable results. Sponsored search represents an important segment of the Internet economy today. In order for search engine providers to offer relevant search results and increase their financial returns, they need to understand the competitive landscape and the implications of different strategies advertisers employ.

The rest of the article is organized as follows. In the next section, we provide a review of related research in search advertising. Then, we present the methodology and the various steps we took for model specification. This will be followed by the results of the PCA-DEA and the efficiency pattern analyses. In the subsequent section, we provide discussions of the results and implications for research and practice. In the final section, we provide concluding remarks and discuss limitations and future research directions.

LITERATURE REVIEW

Most of the published research in search advertising focuses on keyword auction mechanism design and bidding strategies. These studies examine how different agents (i.e., customers who engage in keyword search, advertisers who bid for keywords, and the search brokers who sell ad slots) interact in the auction mechanism. For example, Weber and Zheng (2007) develop a two-stage model to identify a suitable mechanism for search engines, and find that ranking advertisers purely on bid amounts is not optimal for search engines. Liu and Chen (2006) also study alternative ranking rules in keyword auctions by comparing the equilibrium bidding when advertisers are ranked by unit prices versus the product of unit prices and CTR. They show that the latter approach is efficient, though the revenues generated by the two approaches are ambiguously ranked. In an extended setting, Liu et al. (2010) further examine the use of differentiated minimum bids, together with the weighted ranking rule, as a way of exploiting ex ante information on advertisers. These studies highlight the current trends in keyword auction mechanisms in which bidders are evaluated by multiple underlying attributes. They also represent most of the theoretical foundation in the search advertising literature.

In contrast, the literature on the performance of search advertising focuses on keyword selection, performance prediction, and advertisement budget allocation. Rusmevichientong and Williamson (2006) formulate a model of keyword selection and propose algorithms for selecting profitable keywords based on historical performance. Regelson and Fain (2006) predict future CTR by clustering existing advertisements and using the cluster’s historical CTR. Ghose and Yang (2009) analyze the factors that drive differences in sponsored search metrics based on a hierarchical Bayesian modeling framework and using keyword attributes collected from a large nationwide retailer. They find that the monetary value of a click is not uniform across all ad positions because conversion rates are highest at the top and decrease with rank. Their results also indicate that keywords that have more prominent positions on the SERP, and thus experience higher CTR or conversion rates, are not necessarily the most profitable ones. Animesh, Viswanathan, and Agarwal (2011) develop and test a model that predicts the CTR of a seller’s listing, drawing from the consumer search, directional markets, and competitive positioning literatures. Their empirical analysis, based on field data from a firm in the mortgage industry, suggests that CTR is jointly driven by a seller’s positioning strategy, by its rank in a sponsored search listing, and by the nature of competition around the focal firm’s listing. Yang and Ghose (2010) model the interrelationship between organic search listings and paid search advertisements to estimate the effect of organic listings on the CTR of paid search advertisements, and vice versa

for a given firm. Other related studies examine the advertisement budget allocation problem and develop optimization models for allocating expenditures on keyword advertisements (e.g., Kitts & Leblanc, 2004; Fruchter & Dou, 2005; Abrams, Mendelevitch, & Tomlin, 2007; Muthukrishnan, Pal, & Svitkina, 2007; Ozl ¨ uk & ¨ Cholette, 2007; Gopal, Li, & Sankaranarayanan, 2011).

In general, the studies that are related to ad performance represent important steps toward more comprehensive analysis of efficiency in search advertising. Their empirical results highlight the complex relationships among the various metrics in search advertising. Yet many of the past studies focus on a single advertiser and commonly used performance measures such as the CTR. As a result, the analyses and empirical results do not provide complete insights into search advertising performance. In this research, we attempt to understand search advertising practices on a larger scale by examining several retail firms and exploring various resourceand performance related variables that are identified based on current trends in the search industry as well as existing research.

METHODOLOGY

There are two main streams of efficiency evaluation and benchmarking approaches in the literature: nonparametric and parametric. DEA as a nonparametric approach and stochastic frontier analysis (SFA) as a parametric approach are the most commonly used methods (Nieswand, Cullmann, & Neumann, 2010). DEA is a nonparametric method used to empirically measure the relative efficiency of decision making units (DMUs) that use multiple inputs to produce multiple outputs (Charnes, Cooper, & Rhodes, 1978). As a nonparametric method, DEA’s reference technology is not determined by imposing a functional form that describes the production process, but by means of linear programming methods assuming a transformation of inputs into outputs (Nieswand et al., 2010). The basic DEA models consider two types of technology, constant returns to scale (CRS) proposed by Charnes et al. (1978), and variable returns to scale (VRS) suggested by Banker, Charnes, and Cooper (1984).

On the other hand, the SFA, introduced by Aigner, Lovell, and Schmidt (1977), is a regression approach to measuring efficiency. As a parametric method, the SFA determines the reference technology based on econometric methods and assumes a particular functional form for the production process (e.g., Cobb-Douglas or translog function). The SFA is particularly motivated by the fact that non-frontier production can occur because of inefficiency and statistical noise. Accordingly, the approach decomposes the overall error term into inefficiency and traditional error terms, thus allowing for technical efficiency and measurement error. Nevertheless, the decomposition of the overall error relies on the distributions assumed for the two components. Hence, the SFA may produce biased estimates if distributions are chosen for analytical convenience (Ruggiero, 1998). In particular, failure to correctly choose the functional form may produce inefficiency estimates that are confounded with model specification errors. When the exact functional form of the production process is unknown, DEA can accomplish the same objective without requiring explicitly formulated assumptions and variations with different types of models such as in linear and nonlinear regression models (i.e., DEA lets the data speak for itself). Furthermore, the SFA is criticized for handling only one output in efficiency analysis, which limits its applicability in multiple output settings. Banker, Gadh, and Gorr (1993) also provided a Monte Carlo analysis comparing DEA and the SFA. They found that, in cases where statistical noise dominated efficiency, both methods performed poorly; in cases where measurement error was small relative to inefficiency, DEA outperformed the SFA. In general, although DEA has the disadvantage of assuming no statistical noise, it has the advantage of requiring few assumptions about the underlying technology and the capability to handle complex settings with multiple input and output technologies (Jacobs, 2001).

As discussed before, managing search advertising has increasingly become complex, requiring deeper understanding of the various forms of resources as well as the metrics that are utilized to track the performance of ad campaigns. In order to facilitate measurement of efficiency in this multiple input and output environment, we employ DEA as our primary methodology. DEA has a number of advantages over parametric methods that make it a better choice for our study. First, the method is capable of handling multiple inputs and multiple outputs with any input-output measurement, thus overcoming the limitations of traditional efficiency measures that rely on simple ratio analysis. Second, DEA has been proven useful in uncovering relationships that may remain hidden for parametric techniques due to a priori assumptions. DEA can be used even in situations where the relationships between the multiple inputs and multiple outputs are complex or unknown. Therefore, due to the possibility of various forms of relationships among the input and output variables, DEA provides an appropriate fit for the analysis required to address our research objectives. Third, unlike regression-based techniques which base comparisons relative to average performance, DEA bases comparisons relative to an efficiency frontier, thus allowing comparisons with best practices. To reiterate, we believe the task of improving search advertising performance begins with understanding the best practice in one’s competitive circle or peers. Thus, one mechanism for firms to improve their operational efficiency or develop a survival strategy in search advertising is to emulate efficient firms that can be identified by evaluating observed performances. DEA’s empirical orientation toward frontiers makes it a better choice for achieving this end. The method has been applied successfully to various industries. For example, it has been used to measure the relative efficiency of bank branches (Sherman & Gold, 1985; Vassiloglou & Giokas, 1990; Golany & Storbeck, 1999), health care facilities (Banker, Conard, & St´rauss, 1986; Chen, Hwang, & Shao, 2005; Dey, Hariharan, & Clegg, 2006; Prior, 2006), educational services (Mayston, 2003; Banker, Janakiraman, & Natarajan, 2004), software development (e.g., Chatzoglou & Soteriou, 1999), and electronic commerce (Alpar, Porembski, & Pickerodt, 2001; Serrano-Cinca, Fuertes-Callen, & Mar-Molinero, 2005). A comprehensive taxonomy on DEA is also found in Gattoufi, Oral, and Reisman (2004) and Kleine (2004).

DEA Model Specification

Ever since Charnes et al. (1978) introduced the CCR model, several variants of DEA have been used in the literature. Traditional applications of DEA were

predominantly focused on public sector performance assessments using the original CCR model. In recent years, DEA has grown into a powerful analytical tool due to its flexibilities and methodological extensions (Cooper, Seiford, & Zhu, 2004). Because the definition of a DMU is generic and flexible, these extensions facilitate the use of DEA in a great variety of applications to evaluate the performance of entities engaged in many different activities in many different contexts (Cooper et al., 2004). Among the main extensions, the most commonly used is the BCC model (Banker et al., 1984), due to its flexibility in handling VRS. The returns to scale concept, also known as elasticity, represents the relationship between the inputs and the outputs when either of them are changed. Another major aspect of DEA model specification is its orientation (input-oriented or output-oriented). The input-oriented model attributes greater emphasis to a process which aims at utilizing less input for a given level of output. Whereas, the output-oriented model attributes greater emphasis to a process that aims to produce more outputs with a given level of input (Charnes, Cooper, & Rhodes, 1981).

In search advertising, firms usually specify their daily ad budget and other relevant factors in order to maximize the performance of their campaigns as much as possible. In this regard, the output-oriented model provides a better perspective for search advertising. Moreover, the VRS is more suitable for our study, which deals with heterogeneous retail firms representing different sizes, channel types, and merchandizing categories. Therefore, the particular DEA model adopted in this study is the output-oriented BCC model, which can be written in envelopment form as

$Max \phi + \varepsilon \left( \sum_{i=1}^{m} s_i^- + \sum_{r=1}^{s} s_r^+ \right)$

subject to

$\sum_{j=1}^{n} x_{ij} \lambda_{j} + s_{i}^{-} = x_{io}, \quad i = 1, 2, ..., m;$

$\sum_{j=1}^{n} y_{rj} \lambda_{j} - s_{r}^{+} = \phi y_{ro}, \quad r = 1, 2, ..., s;$

$\sum_{j=1}^{n} \lambda_{j} = 1$

$0 \le \lambda_{j}, \quad s_{i}^{-}, \quad s_{r}^{+}, \quad \forall j, i, r \quad j = 1, 2, ..., n.$

There are n DMUs to be evaluated and each DMU consumes varying amounts of m different inputs to produce s different outputs. A given DMU, DMU_j consumes amount $x_{ij}$ of input i and produces amount $y_{rj}$ of output r. The variables $y_{ro}$ and $x_{io}$ are the observed output and input values, respectively, of the DMU to be evaluated (i.e., DMU_j = DMU_o). The $S^-$ and $S^+$ represent slack variables, and the maximal output augmentation is accomplished through $\phi$ . The $\varepsilon$ is a so-called non-Archimedean element defined to be smaller than any positive real number.

The convexity constraint allows VRS evaluations, and a DMU is efficient if and only if φ^∗ = 1 and all slacks are zero.

Selection of input and output variables and theoretical foundations

Recent research in search advertising has examined several keyword advertising metrics in assessing the performance of search engine marketing (SEM) campaigns. These metrics are primarily driven by consumer search behavior and responses to search engine advertising. Unlike traditional advertising, search engine advertising can trigger direct consumer behavioral responses that can be tracked online. As a result, several measures have been recommended and their relationships empirically analyzed in the search advertising literature (Table 1 contains a summary of metrics examined in the SEM literature).

To understand consumer responses to SEM campaigns, Jansen and Schuster (2011) classify keywords into the stages of the buying funnel (i.e., awareness, research, decision, and purchase) and compare the consumer behaviors associated with each stage of the buying funnel using metrics such as impressions, clicks, cost-per-click (CPC), number of orders, number of items purchased, and sales. The buying funnel is a well known paradigm in marketing research for conceptually understanding customer behavior and describing the way consumers make their buying decisions, from awareness of a need all the way to the final purchase of a product or service that addresses this need (Jansen & Schuster, 2011). Their research shows the significance of assessing the performance of SEM campaigns based on consumer reactions in the different stages of the buying funnel. As consumers progress through a buying behavior, advertisers would be engaged in branding to generate impressions and clicks, in addition to converting consumers and generating sales.

In a series of empirical studies, Ghose and Yang (Ghose & Yang, 2007, 2008a, 2009) estimate the effect of sponsored search advertising at a keyword level on consumer search, click, and purchase behavior in electronic markets. Based on a unique panel dataset of several hundred keywords from a Fortune 500 firm that advertises on Google, they empirically model the relationship between different sponsored search metrics such as CTR, conversion rates, CPC, and ranks. They also estimate how keyword-specific characteristics (such as the presence of retailer information and brand information as well as the length of a keyword) affect the above metrics. In Ghose and Yang (2008c, 2010), the authors also evaluate the cross-selling potential of sponsored search by estimating the impact of these keyword attributes on consumer purchase propensities across different categories after clicking on a specific keyword.

Gopal et al. (2011) examine the interaction between the search channel and the content channel in keyword-based advertising using keyword metrics such as impressions, CTR, CPC, and daily ad budget. They find that there is significant cannibalization across the two channels as well as within-channel decreasing returns to impressions. Their empirical analysis reveals that with an increase in the number of impressions on either channel, the CTR for the other channel decreases, and with an increase in the number of impressions on either channel, the CTR for that channel decreases as well. Using a game theoretic model, they further show that when ad

mary of m Su Table 1:	M) literature. marketing (SE metrics in search engine
Literature	Metrics Data and	Methodology	Contributions
mer Jansen and Schuster (2011) The buying funnel and consu M. interaction with SE	per day, sales per day, number of orders per day, number of items Metrics: impressions, clicks, cost Data of nearly 7 million records m a major U.S. retailer. purchased per day fro	and a one-way ANOVA statistical m Keyword classification algorith analysis	Evaluate the effectiveness of the buying funnel as a model for interaction with keyword mer mpaigns. understanding consu advertising ca
Spillover effects of generic to Rutz and Bucklin (2011) branded keywords.	rate (CTR), conversion rate (CR), Metrics: impressions, click-through average position, cost-per-click Keyword-level paid search data m a major lodging chain. (CPC), number of sales fro	M) mic linear model (DL mated in a Bayesian mework esti Dyna fra	Showed that generic keywords have a positive spillover effect on branded keywords through ”awareness of relevance.”
Ghose and Yang (2008c, 2010) sponsored search advertising. Cross-category purchases in	conversion rate, cost-per-click, m a nation-wide rank, keyword type, keyword Panel data in several keyword click-through rate, categories fro retailer. length Metrics:	Hierarchical Bayesian modeling,	mers’ search for products in propensity to buy products within across other product categories in Analyzed the relationship between a specific category and their that category and spillovers me session. consu the sa
Ghose and Yang (2007, 2008a, mpirical analysis of sponsored mance. search perfor 2009) E	conversion rate, cost-per-click, m a rank, keyword type, keyword length, landing page quality Keyword-level panel data fro click-through rate, nation-wide retailer. Metrics:	Monte Carlo Hierarchical Bayesian modeling mation methods Markov chain and esti	metrics and the factors that drive Analyzed the relationship between differences in these metrics. different sponsored search
			Continued

Continued. Table 1:
Literature	Metrics Data and	Methodology	Contributions
Relationship between organic and Ghose and Yang (2008b); Yang sponsored search advertising. and Ghose (2010)	rate, cost-per-click, and keyword mer response to keywords click-through rate, conversion Panel data based on aggregate m a nation-wide retailer. Metrics: search volume, consu ranks fro	Monte Carlo Hierarchical Bayesian modeling mation methods Markov chain and esti	sponsored and organic search mer clicks and advertiser profits. interrelationship between ms of consu Analyzed the nature of the results in ter
Interaction effects between search and content channels. Gopal et al. (2011)	impressions, click-through rate, mpanies over one month period. m eight co rank, daily ad budget. cost-per-click, Daily data fro Metrics:	me Regression analysis and ga theoretic model	mpirically showed the presence of significant cannibalization across mined the mal allocation of budget between the two channels. the two channels. Exa opti E
mance in paid Rutz and Bucklin (2007) Search advertising. Keyword perfor	conversion rate, cost-per-click, Keyword-level paid search data m a major lodging chain. click-through rate, keyword position Metrics: fro	Hierarchical Bayes binary choice model	m. addresses the sparseness proble Developed a model of individual keyword conversion that

budget is very low (very high), it is better to use only the content (search) channel, but it is optimal to utilize both channels otherwise. Further, their model suggests that when the ad budget increases, in order to properly incentivize the service provider, the advertiser should increase the CPC for search, but not for content.

An important consideration when using DEA to assist in efficiency evaluation and benchmarking is the selection of appropriate input and output variables. As highlighted before, the current ad ranking mechanisms require advertisers to perform broadly comparable activities that provide the basis for the transformation of inputs into outputs in our production view of search advertising. In our context, input variables represent the resources (factors) firms employ in their search advertising activities, and output variables represent the outcome of search advertising campaigns in terms of different performance metrics. Consequently, for the input variables, we considered keyword-specific attributes and cost attributes that are relevant for the day-to-day execution of a firm’s search advertising activities. For the keyword-specific attributes, we included the number of paid keywords, number of organic keywords, the length (number of words) in a keyword, and the number of ad copies. For the cost attributes, we included the CPC and the cost-per-day. For the output variables, we included a range of performance measures based on our review of the literature on keyword performance metrics and the consideration of different advertising goals. These include impressions, CTR, paid ad rank percentile, organic rank, as well as conversion rate and online sales attributed to search advertising.

The number of paid keywords and number of organic keywords represent the diversity of words or phrases firms choose to compete in search marketing. Rutz and Bucklin (2007) observe that many of the keywords in paid search campaigns generate few, if any, sales conversions for even several months. They emphasize that this sparseness makes it difficult to assess the profit performance of individual keywords and has led to the practice of managing large groups of keywords together. In order to operationalize their natural search strategies, firms also need to optimize their sites’ contents with individual keywords. Therefore, the number of paid keywords and the number of organic keywords have direct implication on resource utilization because the basic mechanism of paid search advertising operates at the keyword level. In addition, the number of ad copies represents the different versions of ads advertisers prepare in order to effectively link keywords with the contents of ads. Ad copies indicate the degree of ad customization and how advertisers appeal to different buyer needs. Advertisers often craft different copies of an ad due to a limitation in the number of words and the need to target different promotional ideas. They also rotate different ad copies from time to time to reflect seasonality and different pricing strategies. Thus, the number of ad copies also represents advertisers’ efforts and resource utilization in the competition for ad slots.

Similarly, the length of keywords reflects advertisers’ keyword management efforts in order to match the meaning of keywords with ad contents. Advertisers have the option of making the keyword advertisement either generic or specific by altering the number of words contained in the keyword (Ghose & Yang, 2009). In addition to retailer-specific and brand-specific keyword characteristics, Ghose and Yang (2009) examine the length of the keyword as an important determinant of search and purchase behavior. Prior studies have also shown that the percentage of searchers who use a combination of keywords is 1.6 times the percentage of those who use single-keyword queries (Kilpatrick, 2003). Jansen, Booth, and Spink (2008) synthesize prior research and present a broader classification of user intent for Web searching by categorizing user queries in search engines into navigational (e.g., a specific firm or retailer), transactional (e.g., a specific product), or informational (e.g., keywords with longer words). Rutz and Bucklin (2011) also show that there is a strong asymmetric spillover from generic search to branded search activity. They argue that while stand-alone metrics usually show that generic keywords have higher apparent costs to the advertiser than branded keywords, generic search may create a spillover effect on subsequent branded search. Using a Bayesian estimation approach, they show that generic search activity positively affects future branded search activity via “awareness of relevance.” These results have implications for advertisers in their efforts to create an effective portfolio of keywords, not only in terms of the number of keywords to address the diversity of product categories and promotional ideas, but also in terms of the degree of specificity or length of words in a keyword.

Furthermore, the CPC represents advertisers’ payments to the search provider each time a user clicks on their sponsored links. In addition, the cost-per-day represents the observed daily ad expenditure on keywords. Advertisers track their cost-per-day to gauge their expenditures against their maximum daily ad budget. Although both variables represent cost attributes, the use of only one of these variables may not completely capture the dynamics in resource utilization. The two variables represent separate decisions by firms when they sign up for their PPC programs. As requirements, firms select their keywords, specify their daily budget to run their advertisements, and specify the cost they are willing to pay for a click on each keyword. Then, ads are displayed as often as possible while staying within the daily budget. When the daily budget limit is reached, the ads will typically stop showing for that day. Thus, the cost-per-day represents a firm’s average spending during the day, but within the budget limit. However, firms do not necessarily spend on all their keywords every day. They may also follow different spending or bidding strategies. For example, firm A and firm B may both have an average daily spending amount of $500. However, firm A may spend its budget on a few expensive keywords, but firm B may spend the same amount on thousands of inexpensive keywords. In this case, using only the CPC or the cost-per-day on the resource side will ignore the specifics behind the two strategies. Therefore, the assessment of comparative performance becomes more meaningful when both variables are included.

For the performance metrics, the ad rank percentile represents a firm’s ad position in sponsored links, relative to the number of direct competitors for its paid keywords. The higher the ad rank percentile (closer to 100%), the closer to the top the ad position of the firm is for paid keywords. The percentile is preferable because the absolute ad positions for paid keywords may vary significantly depending on whether there are ads in the first three premium slots at the top of the SERP. If there are ads in all premium slots, the ads in the right side of the page begin with position 4. But, if there are none in the premium spots, the first ad on the right side of the page is considered position 1. On the other hand, the organic rank is directly measured in terms of the firm’s average position in natural search results.

Thus, the lower the organic rank value (i.e., closer to 1), the closer to the top the position of the firm is for natural search results. Most advertisers run their PPC advertising along with an SEO strategy. Ghose and Yang (2008b) and Yang and Ghose (2010) empirically analyze the nature of the interrelationship between sponsored and organic search results in terms of metrics such as search volume, CTR, conversion rates, CPC, and keyword ranks. They show that the presence of sponsored and organic listings together results in a synergy that increases the CTR on both listings. Using a controlled field experiment, they validate that total CTR, conversions rates, and revenues in the presence of both paid and organic search listings are significantly higher than those in the absence of paid search advertisements.

Impressions and CTR are the most commonly used ad performance measures. While impressions (also called ad views or exposure) measure the number of times a firm’s ads are displayed in the SERPs, CTR captures the proportion of clicks that are generated from impressions. In addition to impressions and CTR, we also considered conversion rate and online sales attributed to search advertising. Practically, a firm should have its ads displayed and clicked in order to generate conversions and sales. Nevertheless, a firm can have higher impressions and CTR, but lower conversions and sales than its competitors. As a result, we have incorporated the various aspects of performance together in the efficiency evaluation model.

Data collection

The retail firms in our study are identified from the top 500 North American retailers, ranked based on their 2007 online revenue by Vertical Web Media (www.internetretailer.com). The search advertising data are obtained from Velocityscape (www.spyfu.com), a privately held software product and services firm that specializes in providing SEM data. This dataset consists of organizational level and keyword level information for firms advertising on Google. Table 2 provides descriptions of the input (resource) and output (performance) variables included in our study. Table 3 summarizes the descriptive statistics for the variables.

In order to ensure the integrity of the data, extensive preprocessing was performed. Retailers with missing data for the input and output variables were eliminated from the top 500 list. The data contain 14 product categories where each retailer is defined in one category based on its primary business by the data provider. Most of these product categories, however, contain less than ten firms which makes it difficult to design a product level analysis in the current study. We also find that the majority of the retailers are MCRs. Therefore, to maintain equal proportions of merchant types and represent diverse product categories for our study, a final sample of 100 WORs and 100 MCRs were selected. To do so, strata were first formed for both merchant types so that the number of firms under each product category in the sample is maintained proportional to the number in the data. The retailers in the sample were then selected within each product category by maintaining heterogeneity in their revenue ranks. Table 4 summarizes the number of retailers selected by product category for each merchant type.

	Description	Data Source
mber of organic keywords mber of paid keywords Input (Resource) Variables Nu Nu	mpete in keyword auctions. mber of organic keywords a retailer uses to establish its natural mber of paid keywords a retailer uses to co The total nu The total nu	SpyFu SpyFu
Length of keywords Cost-per-click	mber of words that are contained in a retailer’s paid keywords me its ads are clicked on. mount a retailer pays Google each ti ranking via SEO. The average nu The average a	SpyFu SpyFu
mber of ad copies Cost-per-day Nu	mber of ad copies (versions of ads) a retailer maintains for all its ad The average daily spending of a retailer on its keywords (phrases). The total nu groups.	SpyFu SpyFu
mance) Variables Output (Perfor
Online sales	m its online channel. The annual revenue a retailer received fro	Internet Retailer
mpressions I	mes a retailer’s ads are shown (i.e., exposure) as a result meone searching on Google. mber of ti The average nu of so	SpyFu
Click-through rate	mber of clicks a retailer’s ads receive with mes its ads are shown. The average rate representing the nu mber of ti respect to the nu	SpyFu
Conversion rate	Web site that eventually convert or make a The proportion of visitors to a retailer’s purchase.	Internet Retailer
Ad rank percentile	The average ad position of a retailer on its paid keywords that takes into account minating the first position. %) mpetitors. Ad rank percentile close to 1.00 (i.e., 100 main is closer to do indicates that the retailer’s do mber of ad co the nu	SpyFu
Organic rank	The average natural ranking of a retailer on the Google search engine as a result of main is its SEO strategies. A value closer to 1.00 indicates that the retailer’s do closer to the top position in natural search results.	SpyFu
The search marketing data are based on all keywords a fir search engine shoppers in 2007. Note:	Media (www.internetretailer.co Velocityscape (www.spyfu.co Words and was tracked by Web Vertical m 1, 2006 to October 31, 2009. The data for online sales and conversion rate were obtained fro m runs in Google Ad	m) based on m) fro

Table 3: Descriptive statistics.

	Minimum	Maximum	Mean
Input (Resource) variables
Number of paid keywords	72	1,384,081	19,208
Number of organic keywords	28	3,152,589	36,849
Length of keywords	1.90	3.46	2.69
Cost-per-click	$0.15	$0.71	$0.37
Cost-per-day	$10.67	$49,129,800	$415,988
Number of ad copies	941	11,820,588	249,683
Output (Performance) variables
Online sales	$1,714,608	$5,180,000,000	$89,509,777
Impressions	31,070	1,721,873,275	46,557,050
Click-through rate	0.0013	0.0451	0.0081
Conversion rate	0.0005	0.0684	0.0120
Ad rank percentile	0.17	0.79	0.53
Organic rank	6.49	35.81	22.58

Table 4: Number of retailers by product category.

Product Categories	MCRs	WORs
Apparel & accessories	34	8
Books, music, & video	3	5
Computers & electronics	9	14
Food & drug	5	4
Flowers & gifts	3	3
Health & beauty	4	7
Housewares & home furnishing	9	11
Hardware & home improvement	3	10
Jewelry	1	4
Mass merchant	6	7
Office supplies	2	5
Sporting goods	8	4
Specialty items & nonapparel items	9	15
Toys & hobbies	4	3
Total number in sample	100	100

Model specification issues

In order to run the DEA model, we created a data matrix consisting of the six input variables, the six output variables, and the 200 firms as decision-making units (DMUs). The utility of DEA depends on its ability to calculate the relative efficiency of DMUs using multiple inputs and multiple outputs. One common limitation is the potential problem of differentiating DMUs, which may result from the presence of significantly correlated input and output variable sets, or a large number of input and output variables with respect to the total number of DMUs in the analysis (Nunamaker, 1985; Adler & Berechman, 2001). In our first run of the complete model with all the input and output variables, 45% of the firms in the sample were found to be operating at 100% efficiency. We believe this percentage does not portray a realistic picture of the online retailing industry as it implies that a large percentage of the firms in the industry are operating at full efficiency in their search advertising operations. Because we are examining the input and output variables based on observed profiles of the firms in a crosssectional setting, we focus on correlations, rather than directional causality within the input set as well as output set. Therefore, to increase the discriminatory power of DEA in the data, it was necessary to examine the correlations among the input and output variable sets and the adequacy of our sample size. Table 5 summarizes the results of the correlation analysis for our sample data.

For the input set, the correlation analysis suggests that the number of paid keywords has significant positive correlations with the number of organic keywords, cost-per-day, and number of ad copies. The number of organic keywords also has significant positive correlations with the cost-per-day and the number of ad copies. In addition, the cost-per-day has significant positive correlation with the number of ad copies. For the output set, the analysis suggests significant positive correlation between conversion rate and CTR, between impressions and online sales. There is also moderately significant positive correlation between ad rank percentile and the organic rank. Note that the negative sign simply indicates the way the two variables are measured in the data. Moreover, between the input and output variables, we find that the number of paid keywords and organic keywords have significant positive correlations with sales and impressions. The CPC also has significant positive correlations with the conversion rate and the ad rank percentile. Finally, both the cost-per-day and the number of ad copies have significant positive correlations with online sales and impressions.

The presence of significant correlations within the input as well as output sets may indicate redundant information. However, this does not necessarily mean that variables involved in high correlations can be arbitrarily selected or excluded from the analysis without changing the DEA results (Nunamaker, 1985). For example, Jenkins and Anderson (2003) have cautioned that an analysis of simple correlation is insufficient in identifying unimportant variables, and removing even highly correlated variables could have a significant impact on the efficiency scores. In other words, correlation analysis for DEA should not be used purposely for variable elimination as it could lead to possible omission of important variables for efficiency estimates (Jenkins & Anderson, 2003). Experimental evidence on the robustness of DEA has also shown that the effect of omitting relevant inputs on efficiency is more adverse than the inclusion of potentially irrelevant ones (e.g., Galagedera & Silvapulle, 2003). Smith (1997) also analyzed model misspecification from the omission of significant variables and the inclusion of irrelevant variables, and concluded that the dangers of misspecification are most serious when simple models are used and sample sizes are small. In this case, he suggested that it will usually be to the modeler’s advantage to include possibly irrelevant variables rather than exclude a potentially important variable from the model.

Several studies, therefore, suggest that PCA is the most effective procedure for specifying models in the presence of correlations, with the theoretical advantage of enhancing the discerning power of DEA on the resulting efficiency scores

	Correlation analysis. Table 5:
		1	2	3	4	5	6	7	8	9	10	11	12
1	mber of paid keywords Nu	1
2	mber of organic keywords Nu	.978a	1
3	Length of keywords	−.037	−.020	1
4	Cost-per-click	−.060	−.083	.073	1
5	Cost-per-day	.988a	.980a	−.046	−.061	1
6	mber of ad copies Nu	.983a	.944a	−.014	−.044	.948a	1
7	Conversion rate	−.003	−.015	.099	.213a	−.005	−.013	1
8	Online sales	.943a	.916a	.023	.019	.940a	.929a	.026	1
9	mpressions I	.909a	.860a	.005	−.047	.866a	.956a	−.059	.866a	1
10	Click-through rate	.077	.055	−.071	.094	.074	.071	.297a	.073	−.017	1
11	Ad rank percentile	−.004	−.024	−.004	.563a	−.011	.006	.070	.031	.005	.137	1
12	Organic rank	−.077	−.090	.073	−.110	−.091	−.048	−.094	−.043	−.020	−.132	−.153b	1
	bCorrelation is significant at the .05 level (two-tailed). aCorrelation is significant at the .01 level (two-tailed).

(e.g., Adler & Berechman, 2001; Adler & Golany, 2001, 2002; Serrano-Cinca & Mar-Molinero, 2004; Adler & Yazhemsky, 2010). Consequently, we adopt the PCA procedure for the input and output variable sets in order to address the issue of correlations, and at the same time, balance the potential of omitted variables bias on the efficiency estimates.

Another important model specification issue that affects the discerning power of DEA is the sample size. A shortage of observations can create biased estimates because a DMU can be deemed efficient simply because there exist no peers with which to compare it (Pedraja-Chaparro, Salinas-Jimenez, & Smith, 1999). Orme ´ and Smith (1996) also showed that the potential for endogeneity bias (i.e., where one or more input variables are dependent on output measures) in DEA exists and this bias becomes more pronounced with smaller samples (i.e., a sample size of less than 100 in their experiments). Because DEA does not have goodness of fit statistics as guidance for model quality (Pedraja-Chaparro et al., 1999), ensuring data representation with adequate sample size is crucial. Ruggiero (2003) also verified that the effect of endogeneity in DEA is negated as sample size increases (i.e., if the number of DMUs is relatively large when compared to the number of inputs and outputs). In his experimentation, he found that DEA performs moderately well with a sample size of 100, and extremely well with a sample size of 500.

The rule of thumb for the sample size and the number of variables in the DEA literature (e.g., Banker, Charnes, Cooper, Swarts, & Thomas, 1989; Pedraja-Chaparro et al., 1999) is that the number of DMUs should be greater than three times the sum of input and output variables used in the model (i.e., n > 3(m + s)). As a guide for model specification, this requirement is met very well in our application. Therefore, in addition to the PCA procedure, we believe the adequacy of the sample size in our setting (i.e., 200 firms from different merchant and product categories) alleviates the potential effects of the above problems and contributes to the reliability of our efficiency estimates.

PCA-DEA Framework

According to Jenkins and Anderson (2003), two methods for improving the discriminatory power of DEA without the use of additional preferential information exist: (i) variable reduction (VR), and (ii) PCA-DEA. VR reduces the input and output variables based on a partial covariance analysis. This method takes into account the degree of correlation between variables so as to identify the variables that could be omitted with minimal loss of information. PCA-DEA, on the other hand, is used to reduce the number of variables in DEA by aggregating highly correlated variables in the input set and output set separately. Reducing the variables based on PCA not only leads to a parsimonious model, but also increases the discerning capabilities of DEA (Ueda & Hoshiai, 1997; Adler & Golany, 2001, 2002). A recent study by Adler and Yazhemsky (2010) also found that when the “true” efficiency scores are compared to those of PCA-DEA and VR, the former technique produced more accurate results than the latter consistently across numerous variations of tests and dataset sizes.

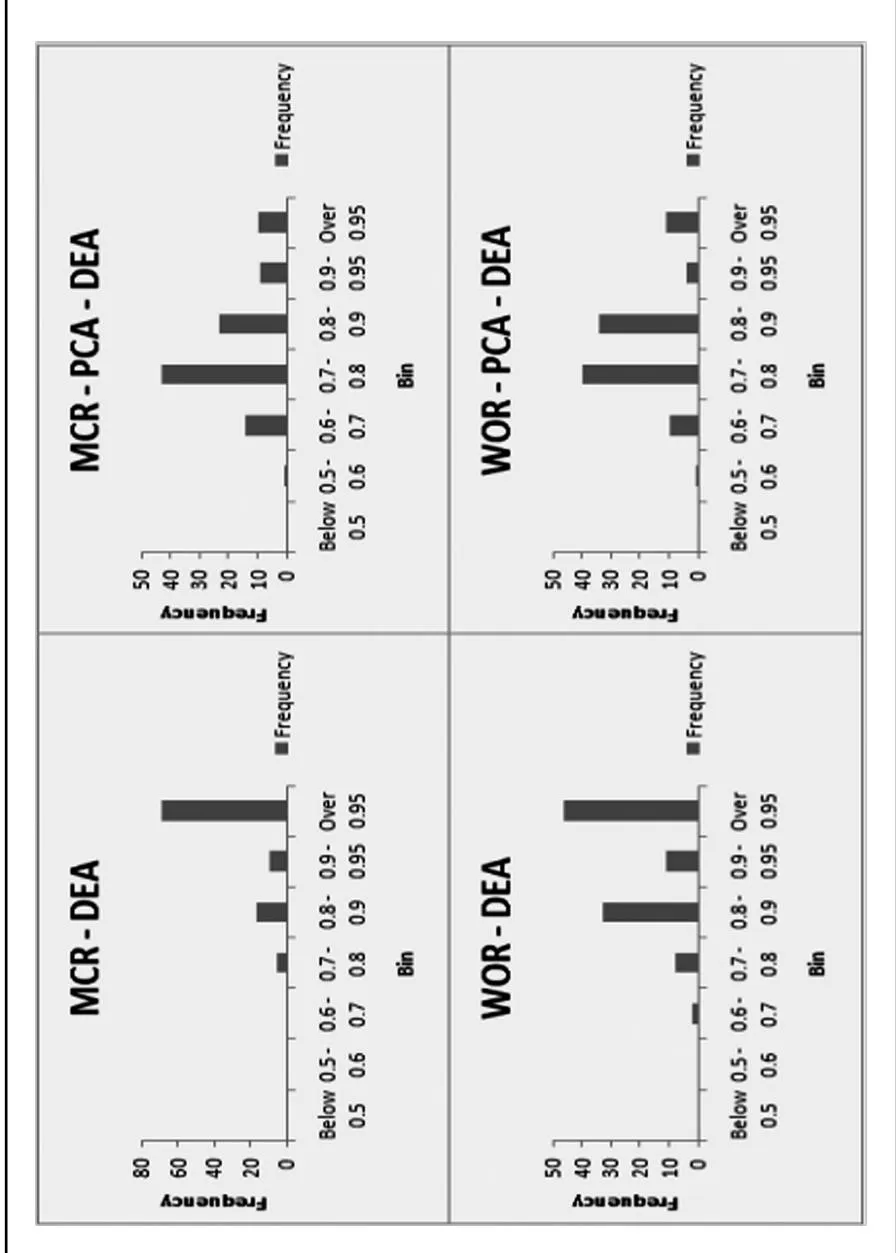
Figure 1 depicts a visualization of the differences in efficiency scores for the two retail merchant categories when DEA was carried out with the original

Figure 1: Comparison of DEA versus PCA-DEA efficiency scores.

Total Variance Explained
	Initial Eigenvalues			Extraction Sums of Squared Loadings
Component	Total	% of Variance	Cumulative%	Total	% of Variance	Cumulative%
1	3.918	65.298	65.298	3.918	65.298	65.298
2	1.068	17.792	83.090	1.068	17.792	83.090
3	0.927	15.455	98.545
4	0.066	1.092	99.637
5	0.020	0.335	99.972
6	0.002	0.028	100.000

Table 6: Total variance explained: input (resource) variables.

variables versus when PCA is applied. The x-axis shows bins for efficiency scores and the y-axis indicates the number of firms.

Note that the efficiencies obtained by DEA are skewed, indicating that the majority of retailers are efficient in their search advertising practices. In contrast, the distribution provided by the PCA-DEA model is in alignment with a study carried out by Forrester Research that revealed that over 50% of merchants are overpaying for keywords, sometimes even paying double the required amount simply to create a barrier on the use of the keywords by other firms (Johnson, Delhagen, & Dash, 2003). Therefore, these results suggest that the PCA-DEA framework is a more realistic approach to evaluate efficiency given the underlying structure of the data. PCA explains the variance covariance structure of a matrix of data through linear combinations of variables, consequently reducing the initial dataset to a few principal components, which generally describe 80–90% of the variance in the data. If most of the variance can be explained by a few principal components, then they can replace the original variables without significant loss of information.

PCA: Input (resource) variables

The use of PCA on the input set led to the extraction of two principal components explaining about 83% of the variance in the dataset. Though the eigenvalue of the third principal component is found to be high relative to that of the fourth principal component, it does not add significant information for variable representation after the extraction of the first two principal components. Table 6 shows the PCA results for the input variables and Table 7 presents the component matrix for the first two principal components. Note also that the first and second principal components have eigenvalues greater than 1, which is the common cut-off point in PCA.

Therefore, PCA on the input set suggests that the first component aggregates the resource variables, number of paid keywords, number of organic keywords, cost-per-day, and number of ad copies (labeled as Tier-1 resources for ease of explanation). The second component aggregates the length of keywords and the CPC (labeled as Tier-2 resources).

Table 7: Component matrix for input variables.

Com	ponent Matrix
	Compo	Component
	1	2
Number of paid keywords	.998	.020
Number of organic keywords	.987	.015
Length of keywords	042	.740
Cost-per-click	086	.719
Cost-per-day	.990	.012
Number of ad copies	.979	.046

Table 8: Total variance explained: output (performance) variables.

Total Variance Explained
	Initial Eigenvalues			Extraction Sums of Squared Loadings
Component	Total	% of Variance	Cumulative%	Total	% of Variance	Cumulative%
1	1.873	31.220	31.220	1.873	31.220	31.220
2	1.456	24.259	55.480	1.456	24.259	55.480
3	1.002	16.706	72.186	1.002	16.706	72.186
4	0.848	14.134	86.320
5	0.694	11.560	97.880
6	0.127	2.120	100.000

Table 9: Component matrix for output variables.

Component Matrix
		Component
	1	2	3
Conversion rate	.011	.662	.505
Online sales	.966	027	.057
Impressions	.958	136	.007
Click-through rate	.092	.720	.311
Ad rank percentile	.072	.482	605
Organic rank	098	498	.531

PCA: Output (performance) variables

Similarly, Table 8 shows the PCA results for the output set. The first three principal components, each with an eigenvalue greater than 1, account for 72% of the variance in the dataset. Table 9 shows the composition of the first three principal components extracted.

Unlike the extraction of components on the input variables, the component matrix for the output variables did not provide a clear representation of the variables

in each principal component. In order to have a better representation of the output variables comprising each principal component, we also verified the results using a rotation. Therefore, PCA on the output set suggests that the first principal component aggregates the performance variables, online sales, and impressions (labeled as Tier-1 metrics); the second component aggregates the performance variables, conversion rate, and CTR (labeled as Tier-2 metrics); and the third component aggregates the performance variables, ad rank percentile, and organic rank (labeled as Tier-3 metrics). Note that the negative sign for the loadings of ad rank percentile and organic rank simply indicates the way the two variables are measured in the data. Thus, their correlation suggests a positive performance link between the two metrics. Unlike click-throughs and conversions, which are measured in rates and are generally low, the sales amounts can be influenced by the average ticket (spending) from a single purchase. For example, Ghose and Yang (2008c, 2010) find that there is a considerable amount of spillover between the initial search and the final purchase behavior such that consumers who begin a search for a product in one category may purchase products from a different category, in addition to purchasing from the original category they searched for. They observed that a single click on a keyword ad may be associated with purchases of different products within a given category or purchases across multiple categories. Thus, from an economic perspective, the advertiser can obtain higher revenues at the same cost. Therefore, the correlation of impressions and sales in our data implies that firms with high impressions are associated with high brand awareness which may contribute to positive perception and influence consumers to spend more in a single purchase. Jansen and Schuster (2011) also state that one makes potential consumers aware of a brand both before and during a desire to purchase, thus advertisers would be engaged in branding, generating a large number of impressions. This would create a positive influence on consumer spending in a single purchase.

Following the PCA procedure, the original variables are replaced by the principal components. Generally, inputs and outputs of a DEA need to be strictly positive. However, the results of PCA can be negative. An affine transformation of the data can be utilized with no change in the results when using standard radial CRS and VRS DEA models (Charnes et al., 1978; Banker et al., 1984). In other words, using the extracted principal components in place of the original data does not affect the properties of the DEA models. Principal components represent the selection of a new coordinate system obtained by rotating the original system. Because it is not a parallel translation of the coordinate system, PCA-DEA could be applied to all basic DEA models (Adler & Yazhemsky, 2010). Due to the translation invariance of the DEA models, the principal components can be increased by the most negative number in the vector plus 1 when necessary, thus ensuring strictly positive data.

With two input components and three output components, our next step involves specifying the PCA-DEA model. The simplest option will be to specify the full model that involves all the input and output components together for efficiency analysis. However, examining efficiency using alternative specifications using subsets of the input and output components can reveal useful information about the DMUs. In addition, retailers that are efficient under one model specification are not necessarily efficient under other model specifications. Thus, alternative

AB1	AB2	AB3
A12	B12	AB12
A13	B13	AB13
A23	B23	AB23
A123	B123	AB123

Table 10: PCA-DEA model specifications.

specifications show the robustness of our efficiency evaluation framework and allow us to examine under which combinations of inputs and outputs a particular retailer performs well. This approach also provides us with information regarding the input and output components that reveal differences in efficiency among the retailers as well as between the merchant types. Accordingly, 15 different DEA models are specified as shown in Table 10, excluding models with only one input and one output variable, as these models represent simple ratio analysis. To distinguish these models, we labeled the components as follows: we use the label A for Tier-1 resources, B for Tier-2 resources, 1 for Tier-1 metrics, 2 for Tier-2 metrics, and 3 for Tier-3 metrics.

Using the output-oriented BCC setting, we first compute the efficiency scores of the retailers under all model specifications. Thus, for each firm and every model specification, we obtain the efficiency score. Then, we analyze the resulting multivariate data using a procedure known as property fitting (Schiffman, Reynolds, & Young, 1981; Serrano-Cinca et al., 2005; Ho & Wu, 2009).

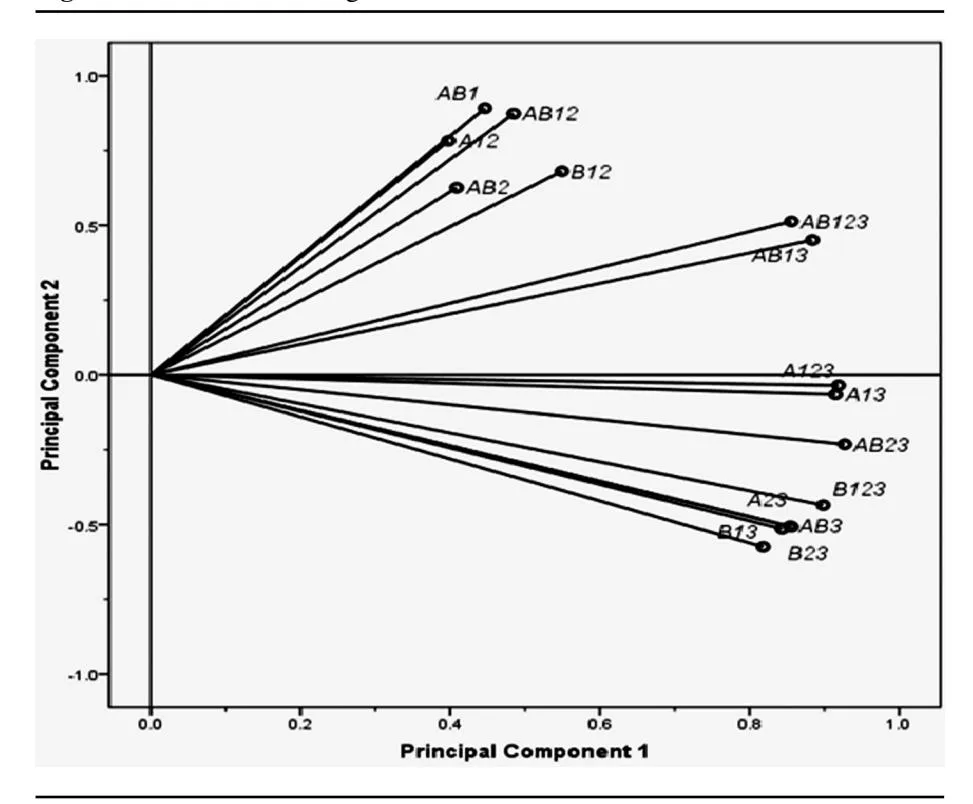
Property Fitting and Efficiency Pattern Analysis

Originally proposed by Schiffman et al. (1981), property fitting (Pro-Fit for short) is a regression-based multidimensional scaling (MDS) technique. We use this technique to examine patterns in efficiency scores from alternative model specifications as demonstrated by Serrano-Cinca et al. (2005) and Ho and Wu (2009). The analysis involves a PCA procedure on the efficiency scores from all model specifications, followed by a visualization procedure that graphically shows the degree of congruity among the models. To conduct the PCA on the models, the different model specifications are defined as variables and the retailers as observations. The goal is to assess which combinations of inputs and outputs (i.e., model specifications) are equivalent. Thus, the extracted components from the PCA help to visualize the similarities and differences that exist between the different DEA models and the most salient efficiency characteristics of the individual firms. This procedure extracted three principal components with eigenvalues greater than 1, and accounting for 90% of the total variance (Table 11). The first principal component accounts for 53% of the total variance, the second accounts for 28% of the total variance, and the third accounts for 8% of the total variance. The interpretation of the principal components is based on the information in the component loading matrix, which is shown in Table 12.

In the component loading matrix, the model specifications are arranged in descending order according to the first principal component. In the first principal component, all the models load with a positive sign on the component. Thus, the

Table 11:	Total	variance	explained:	DEA	model	specification	s.

	Total Variance Explained
	Initial Eigenvalues			Extraction Sums of Squared Loadings
Component	Total	% of Variance	Cumulative%	Total	% of Variance	Cumulative%
1 2	7.981 4.269	53.208 28.462	53.208 81.670	7.981 4.269	53.208 28.462	53.208 81.670
3 4	1.210 0.771	8.067 5.140	89.737 94.877	1.210	8.067	89.737
5 15	0.373 0.001	2.489 .009	97.366 100.000

Table 12: Component matrix: DEA model specifications.

	Component
Model	1	2	3
A13	.900	_	391
A123	.900	_	384
AB23	.877	219	.278
B123	.851	412	_
A23	.835	495	_
AB13	.830	.423	116
B23	.823	502	.150
AB123	.816	.489	_
AB3	.804	476	.114
B13	.770	541	_
AB12	.476	.857	_
B12	.462	.572	.407
AB1	.416	.831	_
AB2	.394	.603	.640
A12	.358	.704	430

first principal component can be interpreted as an overall measure of efficiency (Serrano-Cinca et al., 2005; Ho & Wu, 2009). In the second principal component, the models with high positive loadings only incorporate Tier-1 metrics (i.e., online sales and impressions) and/or Tier-2 metrics (i.e., conversion rate and CTR) in their definitions. On the other hand, the models with negative loadings incorporate Tier-3 metrics (i.e., ad rank percentile and organic rank), in addition to Tier-1 and/or Tier-2 metrics. Therefore, the second principal component provides a differentiation between DMUs that only maximize metric groups Tier-1 and/or Tier-2 versus those that also maximize Tier-3 metrics. In the third principal component, all the negative loadings include Tier-1 metrics, whereas the most positive loadings include Tier-2 metrics. Therefore, the third principal component provides a differentiation between DMUs that maximize Tier-1 metrics versus those that maximize Tier-2 metrics.

Examining the component scores further reveals how efficient each retailer is under each model (Serrano-Cinca et al., 2005; Ho & Wu, 2009). To do so, vectors are drawn in such a way that, for a particular DEA model, the efficiency value obtained increases in the direction of the vector. The direction of the vector is calculated based on a regression model, which is estimated using the efficiency scores derived from a particular model as a dependent variable and the component scores as independent variables. Models that are congruent are identified by means of correlation. Hence, the angle between any two models indicates how similar they are in terms of the patterns of their results. Such models can be interchangeable to describe relative efficiency. In order to ensure the validity of the models, vectors are included only if they are significant and their coefficient of determination is deemed high enough. Despite the numerous DMUs in our study, the lowest R2 value is 0.702, which indicates a good fit for all the models. As a result, we included all the models in the Pro-Fit analysis. The results of the Pro-Fit regression, the directional cosines, and their significance levels are shown in Table 13. Figure 2 also shows the vector diagram from the Pro-Fit analysis. As shown, all the vectors point out toward the right, indicating the correlation among the various paths to efficiency. Therefore, DMUs achieve efficiency through various combinations of variables, particularly with the output variables. However, as far as DMU ranking is concerned, no single model should contribute solely to the position of a DMU, because alternative paths need to be considered when ranking DMUs.

The complete results of the Pro-Fit analysis can easily be visualized in a two-dimensional efficiency map using the first two principal components. This plot provides interesting patterns. To avoid cluttering of the plot, we show the retailers that have positive scores along the first principal component in two separate efficiency maps (Figures 3 and 4). Figure 3 shows the retailers that have lower overall efficiency, and Figure 4 shows the retailers that have higher overall efficiency, as indicated by their position along the first principal component value. In order to show the various paths the retailers follow in achieving efficiency, the vector diagram (i.e., Figure 2) is also superimposed on the efficiency maps.

DISCUSSION

Figures 3 and 4 show the efficiency patterns and the models that reveal these differences, along with the names of the retailers and their merchant categories. In both maps, the retailers that appear on the extreme left have a relatively lower degree of overall efficiency than those that appear on the right (Serrano-Cinca & Mar-Molinero, 2004). In terms of overall efficiency, MCRs occupy most of the top positions. As Table 14 shows, out of the top 30 retailers, 18 are MCRs (see also their efficiency scores on the full model specification—AB123). The top positions include well-established MCRs such as OfficeMax Inc., Staples Inc., Sears Holdings Corp., and Walmart Stores Inc., as well as Amazon.com (from the WORs category). Note also that the MCR 1–800-Flowers.com Inc. and the WOR Beach Audio Inc. are located at the extreme right in Figure 4. These retailers are the most efficient retailers, ranked first and second, respectively, in terms of

TO 11 10	D C 11
Table 13:	Pro-fit linear	regression results.

Models	Gamma 1 $(\gamma_1)$	Gamma 2 $(\gamma_2)$	Gamma 3 (γ 3 )	F	R Sq.	Adj. R Sq.
AB1	0.45	0.89	-0.08	434.46	0.869	0.867
	$(16.123)^{b}$	$(32.185)^{b}$	$(-2.745)^{a}$
AB12	0.48	0.87	0.04	1,684.88	0.963	0.962
	$(34.477)^{b}$	$(62.117)^{b}$	$(2.744)^{a}$
A12	0.40	0.78	-0.48	277.73	0.810	0.807
	$(11.482)^{b}$	$(22.598)^{b}$	$(-13.809)^{b}$
B12	0.55	0.68	0.48	157.51	0.707	0.702
	$(11.944)^{b}$	$(14.797)^{b}$	$(10.531)^{b}$
A123	0.92	-0.04	-0.39	1,540.41	0.959	0.959
	$(62.482)^{b}$	(-2.416)	$(-26.672)^{b}$
A13	0.92	-0.07	-0.40	1,963.27	0.968	0.967
	$(70.231)^{b}$	$(-5.031)^{b}$	$(-30.530)^{b}$
AB13	0.88	0.45	-0.12	489.90	0.882	0.881
	(33.893) b	$(17.274)^{b}$	$(-4.750)^{b}$
AB123	0.86	0.51	-0.06	643.71	0.908	0.906
	$(37.627)^{b}$	$(22.531)^{b}$	$(-2.770)^{a}$
AB23	0.93	-0.23	0.29	557.88	0.895	0.894
	$(37.938)^{b}$	$(-9.479)^{b}$	$(12.020)^{b}$
AB3	0.85	-0.51	0.12	509.26	0.886	0.885
	$(33.394)^{b}$	$(-19.758)^{b}$	$(4.716)^{b}$
B23	0.84	-0.51	0.15	1,284.87	0.952	0.951
	(52.377) b	$(-31.933)^{b}$	$(9.571)^{b}$
A23	0.86	-0.51	0.09	1,233.92	0.950	0.949
	(52.107) b	$(-30.888)^{b}$	$(5.704)^{b}$
AB2	0.41	0.63	0.66	848.27	0.928	0.927
	$(20.614)^{b}$	(31.558) b	(33.526) b
B13	0.82	-0.57	-0.02	508.29	0.886	0.884
	(31.956) b	$(-22.434)^{b}$	(-0.645)
B123	0.90	-0.44	0.06	572.48	0.898	0.896
	(37.239) b	$(-18.031)^{b}$	(2.356)

^<sup>aSignificant at the .01 level (two-tailed test).

overall efficiency. These retailers also achieved 100% efficiency in the majority of the models, which contributes to their rank in the overall efficiency along the first principal component.

Although all the resource variables and performance metrics contribute to the relative efficiency of the retailers to a certain degree, the Pro-Fit analysis shows that some of the variables are more important in revealing differences in efficiency, particularly between the two merchant categories. One interesting pattern to note is that models that load positively and highly on the second principal component include Tier-1 and/or Tier-2 metrics (Figure 2). On the other hand, models that load negatively on the second component all involve Tier-3 metrics. As shown in the efficiency maps, Tier-1 metrics (i.e., online sales and impressions) and Tier-2 metrics (CTR and conversion rate) reveal differences in efficiency mainly for

^<sup>bSignificant at the .05 level (two-tailed test).

MCRs. Note that the retailers that are positioned and associated with the models in the upper left corner of the efficiency maps are predominantly MCRs. On the other hand, Tier-3 metrics (i.e., organic rank and ad rank percentile) reveal differences in efficiency mainly for WORs. Although we cannot say that Tier-1 and Tier-2 metrics are irrelevant for WORs, all the models that involve Tier-3 metrics are associated mostly with WOR on the efficiency maps, thus indicating the importance of these metrics in differentiating the relative efficiency of WORs. As can be seen in the efficiency maps, the retailers that are positioned and associated with the models in the lower right corner are predominantly WORs.

The component loading patterns from our PCA results do not show any discernible difference between the two merchant categories for the input side. As discussed above, our results show differences mainly on the output side. For example, the Pro-Fit vector diagram (Figure 2) shows the congruence among the models A12, B12, and AB12, and also among the models A23, B23, and AB23. These similarities in the efficiency patterns indicate that there is no visible specialization on the use of the inputs between the two merchant categories. Therefore, the Tier-1 and Tier-2 resource components can be used either individually or together to compare relative efficiencies.

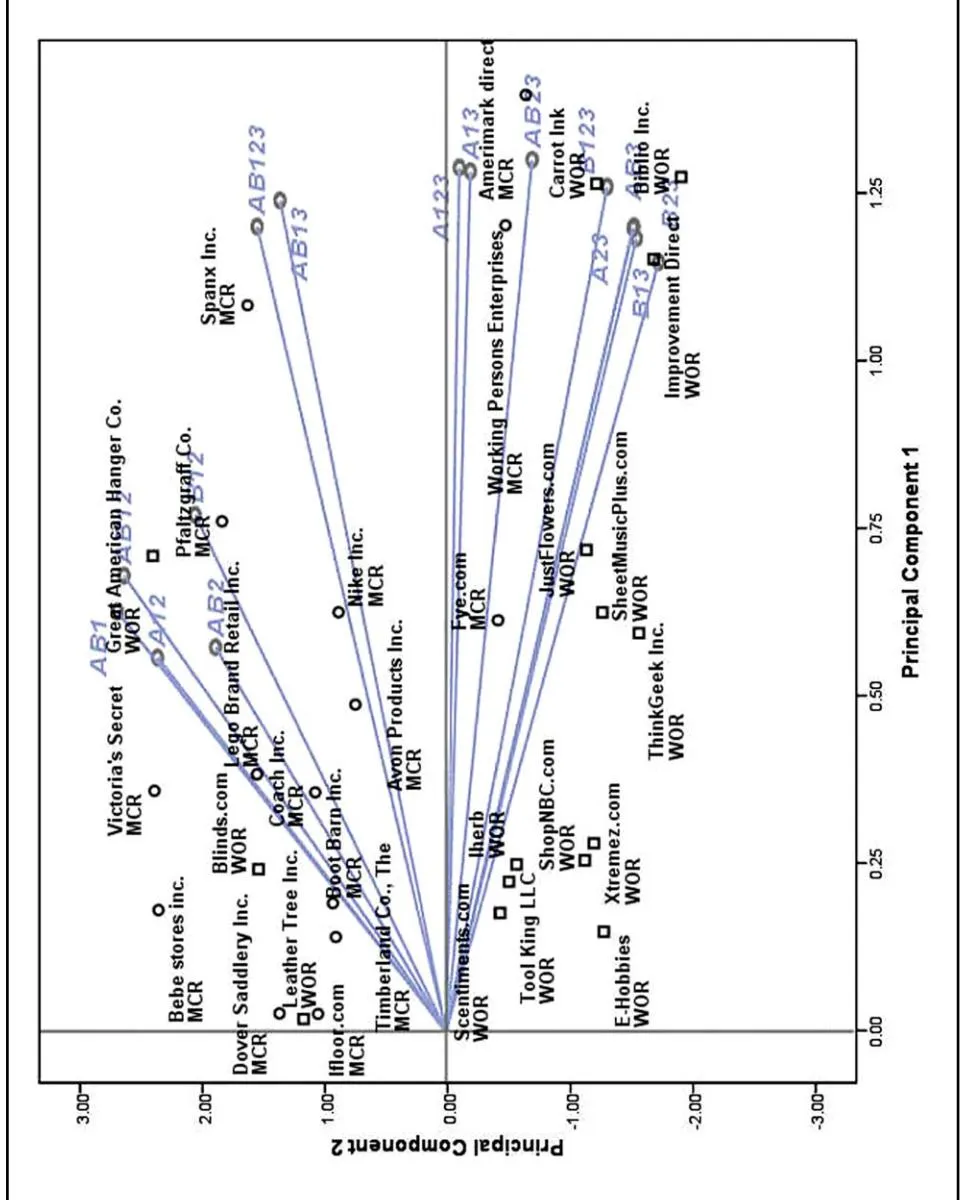
Figure 4: Pro-fit vector diagram and efficiency map-2 (higher overall efficiency).

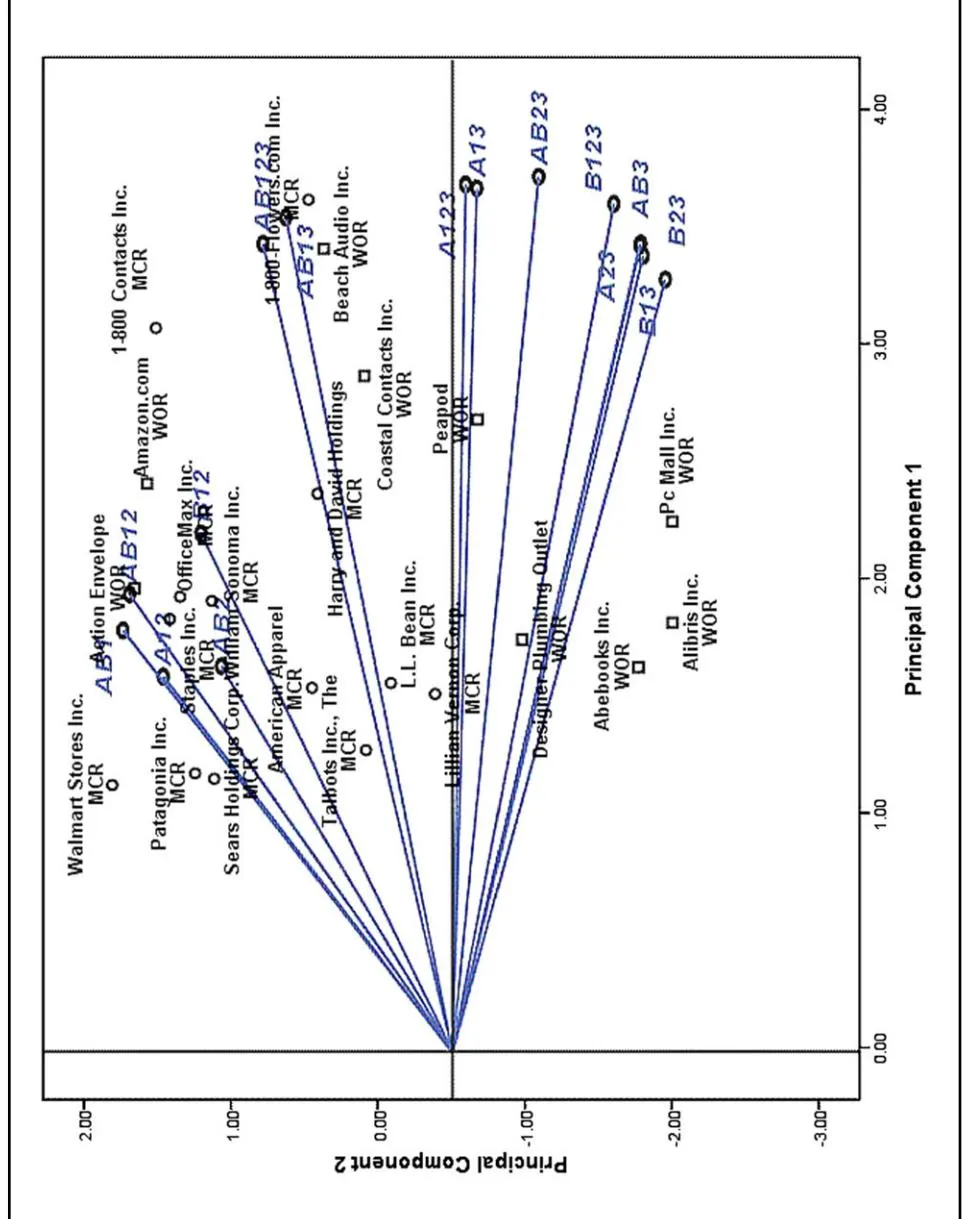
Table 14: Top 30 retailers in terms of overall efficiency (PC-1 values).

Rank	Unit (Retailer) Name	Merchant Type	Component Score: PC-1	Full Model - AB123
1	1–800-Flowers.com Inc.	MCR	3.61	1.00
2	Beach Audio Inc.	WOR	3.41	1.00
3	1–800 Contacts Inc.	MCR	3.07	1.00
4	Coastal Contacts Inc.	WOR	2.86	1.00
5	Peapod	WOR	2.68	1.00
6	Amazon.com	WOR	2.40	1.00
7	Harry and David Holdings	MCR	2.36	0.97
8	PC Mall Inc.	WOR	2.24	1.00
9	Action Envelope	WOR	1.96	1.00
10	OfficeMax Inc.	MCR	1.92	1.00
11	William-Sonoma Inc.	MCR	1.90	1.00
12	Staples Inc.	MCR	1.83	1.00
13	Alibris Inc.	WOR	1.81	0.93
14	Designer Plumbing Outlet	WOR	1.74	0.96
15	Abebooks Inc.	WOR	1.62	0.90
16	L.L. Bean Inc.	MCR	1.55	0.89
17	Fingerhut Direct Marketing Inc.	MCR	1.55	0.91
18	American Apparel	MCR	1.53	0.93
19	Lillian Vernon Corp.	MCR	1.51	0.89
20	Amerimark direct	MCR	1.40	0.87
21	Biblio Inc.	WOR	1.27	0.88
22	Talbots Inc., The	MCR	1.27	0.89
23	Carrot lnk	WOR	1.26	0.93
24	Working Persons Enterprises	MCR	1.20	0.86
25	Patagonia Inc.	MCR	1.17	0.96
26	Restoration Hardware Inc.	MCR	1.16	0.87
27	Improvement Direct	WOR	1.15	0.87
28	Levenger Co.	MCR	1.15	0.86
29	Sears Holdings Corp.	MCR	1.15	0.96
30	Walmart Stores Inc.	MCR	1.12	1.00

Implications for Research

This study contributes to academic research in various ways. First, the study involves extensive analysis on actual data that encompasses online retailers in different merchandizing categories. The results offer a unique, data-driven characterization on the comparative performance of firms in search advertising. Previous research in search advertising has been characterized by lack of an empirical base involving multiple firms. This research is, therefore, an important step in the search advertising literature, not only due to the extensive nature of the data in use, but also the range of quantitative techniques applied in generating efficiency profiles. In particular, this article provides the first large scale empirical assessment of the productivity of online retailers in search advertising. In addition, this study uses multiple resource- and performance-related variables that are drawn from both industry and prior literature in an exploratory bid to identify the key variables that

can explain efficiency in search advertising for online retailers. The results also shed some insight into conventional assumptions on performance-based ad ranking mechanisms.

Implications for Practice

Managerial issues regarding resource allocation, performance evaluation, and benchmarking are important aspects of search advertising campaigns. Indeed various online tools exist in the market today, which provide keyword generation and performance tracking capabilities. Yet these tools come with traditional notions about the evaluation of sponsored search campaigns. Most of these tools focus only on commonly recognized metrics such as the click-through-rate. Given that the rule of the game has been changed by the search providers, advertisers need alternative methods for performance evaluation and benchmarking that take into account the dynamics of search advertising today. Therefore, this study sheds light on the variables that are relevant and key for these objectives.

The increasing availability of real-time data on search advertising requires appropriate techniques in order for firms to monitor the impact of their decisions, benchmark their relative performance against best practices, and improve their overall search marketing programs. Therefore, the methodology and results of this study can inform the search advertising industry of the performance metrics that are important in different merchant categories. Managers in different industries and product categories can also replicate the analytical procedure demonstrated in this study, not only to track their performance, but also to constantly benchmark their performance against the best practice. Furthermore, managers can follow a more tailored approach to this analysis by focusing on the variables that are directly relevant to their competitive environment.

CONCLUSION

This research provides useful information about organizational level understanding of the search advertising practices. We explored several resource- and performancerelated variables that can be used to evaluate and benchmark performance in search advertising. We identified the key variables that reveal differences in efficiency in search advertising. In addition, we examined the variations in efficiency patterns between merchant types in online retailing. As our analysis shows, historical ad positions both in organic and sponsored links are key performance metrics for the efficiency of WORs. Hence, WORs should pay attention to their ad positions both in organic and paid links in order to benchmark their performance against their competitors. On the other hand, the differences in efficiency for MCRs are explained by a range of performance metrics as measured by Tier-1 and Tier-2 metrics. These include not only impressions and CTR, but also conversion rates and sales.

Limitations and Future Research Directions

Due to the highly competitive and dynamic nature of the sponsored search advertising market, future research holds a truly exciting prospect. This study could be extended in a number of ways. First, our data represent the top revenue-ranked retailers in online retailing. However, even within this target group, our sampling procedure maintained heterogeneity in the revenue ranks and we have observed noticeable variations along several performance dimensions. Future research can extend the performance evaluation and benchmarking to a more granular level to examine efficiency patterns across product and service categories.

In terms of methodology, one major pitfall of using DEA is its sensitivity to variations in data. Given its data-driven nature, changes in data as well as correlations among input and output variables can possibly affect the results of a DEA. However, the use of PCA-DEA has the advantage of reducing the impact of significant correlations by extracting and leveraging the internal structure of the data. Another limitation of DEA is its lack of goodness of fit statistics for model quality. As a result, we have attempted to minimize possible model specification errors by (i) applying PCA on the input and output variable sets to control the effect of correlations on efficiency estimates, (ii) ensuring data representation with adequate sample size, (iii) analyzing alternative model specifications and showing robustness with respect to specification, and (iv) identifying the most salient efficiency characteristics of the retailers based on the efficiency pattern analysis. Future empirical research could analyze the exact form of the functional relationships among the variables examined in this research.

REFERENCES

• Abrams, Z., Mendelevitch, O., & Tomlin, J. (2007). Optimal delivery of sponsored search advertisements subject to budget constraints. Proceedings of the 8th ACM Conference on Electronic Commerce, San Diego, CA: ACM New York, 272–278.
• Adler, N., & Berechman, J. (2001). Measuring airport quality from the airlines’ viewpoint: An application of data envelopment analysis. Transport Policy, 8(3), 171–181.
• Adler, N., & Golany, B. (2001). Evaluation of deregulated airline networks using data envelopment analysis combined with principal component analysis with an application to Western Europe. European Journal of Operational Research, 132(2), 260–273.
• Adler, N., & Golany, B. (2002). Including principal component weights to improve discrimination in data envelopment analysis. The Journal of the Operational Research Society, 53(9), 985–991.
• Adler, N., & Yazhemsky, E. (2010). Improving discrimination in data envelopment analysis: PCA–DEA or variable reduction. European Journal of Operational Research, 202(1), 273–284.
• Aigner, D. J., Lovell, C. A. K., & Schmidt, P. (1977). Formulation and estimation of stochastic frontier production function models. Journal of Econometrics, 6(1), 21–37.

Alpar, P., Porembski, M., & Pickerodt, S. (2001). Measuring the efficiency of website traffic generation. International Journal of Electronic Commerce, 6(1), 53–74.

• Animesh, A., Ramachandran, V., & Viswanathan, S. (2010). Quality uncertainty and the performance of online sponsored search markets: An empirical investigation. Information Systems Research, 21(1), 190–201.

• Animesh, A., Viswanathan, S., & Agarwal, R. (2011). Competing “creatively” in sponsored search markets: The impact of rank, unique selling proposition, and competition on the effectiveness of sponsored search listings. Information System Research, 22(1), 153–169.

• Banker, R. D., Charnes, A., & Cooper, W. (1984). Some models for estimating technical and scale inefficiencies in data envelopment analysis. Management Science, 30(9), 1078–1092.

• Banker, R., Charnes, A., Cooper, W. W., Swarts, J., & Thomas, D. A. (1989). An introduction to data envelopment analysis with some of its models and their uses. Research in Governmental and Non-profit Accounting, 5, 125– 164.

• Banker, R. D., Conrad, R. F., & St´rauss, R. P. (1986). A comparative application of data envelopment analysis and translog methods: An illustrative study of hospital production. Management Science, 32(1), 30–44.

• Banker, R. D., Gadh, V. M., & Gorr, W. L. (1993). A Monte Carlo comparison of two production frontier estimation methods: Corrected ordinary least squares and data envelopment analysis. European Journal of Operational Research, 67(3), 332–343.

• Banker, R. D., Janakiraman, S., & Natarajan, R. (2004). Analysis of trends in technical and allocative efficiency: An application to Texas public school districts. European Journal of Operational Research, 154(2), 477– 491.

• Charnes, A., Cooper, W., & Rhodes, E. (1978). Measuring the efficiency of decision making units. European Journal of Operational Research, 2(6), 429– 444.

• Charnes, A., Cooper, W., & Rhodes, E. (1981). Evaluating program and managerial efficiency: An application of data envelopment analysis to program follow through. Management Science, 27(6), 668–697.

• Chatzoglou, P. D., & Soteriou, A. C. (1999). A DEA framework to assess the efficiency of the software requirements capture and analysis process. Decision Sciences, 30(2), 503–531.

• Chen, A., Hwang, Y., & Shao, B. (2005). Measurement and sources of overall and input inefficiencies: Evidences and implications in hospital services. European Journal of Operational Research, 161(2), 447– 468.

• Chen, J., Liu, D., & Whinston, A. B. (2009). Auctioning keywords in online search. Journal of Marketing, 73(4), 125–141.

• Cooper, W. W., Seiford, L. M., & Zhu, J. (2004). Data envelopment analysis: History, models and interpretations. In W. W. Cooper, L. M. Seiford, & J. Zhu (Eds.), Handbook on data envelopment analysis. Boston, MA: Kluwer Academic Publisher, 1–39.

• Dey, P. S., Hariharan, S., & Clegg, B. T. (2006). Measuring the operational performance of intensive care units using the analytic hierarchy process approach. International Journal of Operations & Production Management, 26(8), 849– 865.

• Fruchter, G. E., & Dou,W. (2005). Optimal budget allocation over time for keyword ads in Web portal. Journal of Optimization Theory and Applications, 124(1), 157–174.

• Galagedera, D. U. A., & Silvapulle, P. (2003) Empirical evidence on robustness of data envelopment analysis. Journal of the Operational Research Society, 54(6), 654–660.

• Gattoufi, S., Oral, M., & Reisman, A. (2004). A taxonomy for data envelopment analysis. Socio-Economic Planning Sciences, 38(2–3), 141–158.

• Ghose, A., & Yang, S. (2007). An empirical analysis of paid placement in online search advertising. Proceedings of the ACM International Conference on Electronic Commerce (ICEC 2007), Minneapolis, MN: ACM New York, 95–96.

• Ghose, A., & Yang, S. (2008a). An empirical analysis of sponsored search performance in search engine advertising. Proceedings of the ACM International Conference on Web Search and Data mining Conference (WSDM 2008), New York, NY: ACM New York, 241–250.

• Ghose, A., & Yang, S. (2008b). Comparing performance metrics in organic search with sponsored search advertising. Proceedings of the 2nd Annual International Workshop on Data mining and Audience Intelligence for Advertising (ADKDD 2008), Las Vegas, NV: ACM New York, 18–26.

• Ghose, A., & Yang, S. (2008c). Analyzing search engine advertising: Firm behavior and cross-selling in electronic markets. Proceedings of the World Wide Web Conference (WWW 2008), Beijing, China: ACM New York, 219– 226.

• Ghose, A., & Yang, S. (2009). An empirical analysis of search engine advertising: Sponsored search in electronic markets. Management Science, 55(10), 1605– 1622.

• Ghose, A., & Yang, S. (2010). Modeling cross-category purchases in sponsored search advertising, accessed June 5, 2012, available at SSRN: http://ssrn.com/abstract=1312864 or http://dx.doi.org/10.2139/ ssrn.1312864.

• Golany, B., & Storbeck, J. E. (1999). A data envelopment analysis of the operational efficiency of bank branches. Interfaces, 29(3), 14–26.

• Gopal, R., Li, X., & Sankaranarayanan, R. (2011). Online keyword based advertising: Impact of ad impressions on own-channel and cross-channel clickthrough rates. Decision Support Systems, 52(1), 1–8.

Ho, C.-T. B., & Wu, D. D. (2009). Online banking performance evaluation using data envelopment analysis and principal component analysis. Computers & Operations Research, 36(6), 1835–1842.

• Jacobs, R. (2001). Alternative methods to examine hospital efficiency: Data envelopment analysis and stochastic frontier analysis. Health Care Management Science, 4(2), 103–115.

• Jansen, B. J., Booth, D. L., & Spink, A. (2008). Determining the informational, navigational, and transactional intent of Web queries. Information Processing & Management, 44(3), 1251–1266.

• Jansen, B. J., & Mullen, T. (2008). Sponsored search: An overview of the concept, history, and technology. International Journal of Electronic Business, 6(2), 114–131.

• Jansen, B. J., & Schuster, S. (2011). Bidding on the buying funnel for sponsored search and keyword advertising. Journal of Electronic Commerce Research, 12(1), 1–18.

• Jenkins, L., & Anderson, M. (2003). A multivariate statistical approach to reducing the number of variables in data envelopment analysis. European Journal of Operational Research, 147(1), 51–61.

• Johnson, C., Delhagen, K., & Dash, A. (2003). Retailers: Quit wasting search engine dollars. Forrester Research, accessed July 12, 2009, available at http://www.internetretailer.com/dailyNews.asp?id=8909

• Kilpatrick, D. (2003). Keyword advertising on a cost-per-click model, accessed June 5, 2012, available at http://www.sitepronews.com/ archives/2003/feb/14prt.html.

• Kitts, B., & LeBlanc, B. (2004). Optimal bidding on keyword auctions. Electronic Markets, 14(3), 186–201.

• Kleine, A. (2004). A general model framework for DEA. Omega, 32(1), 17–23.

• Liu, D., & Chen, J. (2006). Designing online auctions with past performance information. Decision Support Systems, 42(3), 1307–1320.

• Liu, D., Chen, J., & Whinston, A. B. (2010). Ex ante information and the design of keyword auctions. Information Systems Research, 21(1), 133–153.

• Mayston, D. J. (2003). Measuring and managing educational performance. Journal of the Operational Research Society, 54(7), 679–691.

• Muthukrishnan, S., Pal, M., & Svitkina, Z. (2007). Stochastic models for budget optimization in search-based advertising. In X. Deng, & F. C. Graham (Eds.), Proceedings of the 3rd international conference on Internet and network economics (WINE). Verlag, Berlin, Heidelberg: Springer, 131–142.

• Nieswand, M., Cullmann, A., & Neumann, A. (2010). Overcoming data limitations in nonparametric benchmarking: Applying PCA-DEA to natural gas transmission. Review of Network Economics, 9(2), Article 4.

• Nunamaker, T. R. (1985). Using data envelopment analysis to measure the efficiency of non-profit organizations: A critical evaluation. Managerial and Decision Economics, 6(1), 50–58.

• Orme, C., & Smith, P. (1996). The potential for endogeneity bias in data envelopment analysis. Journal of the Operational Research Society, 47(1), 73–83.

• Ozl ¨ uk, ¨ O., & Cholette, S. (2007). Allocating expenditures across keywords in ¨ search advertising. Journal of Revenue and Pricing Management, 6(4), 347– 356.

• Pedraja-Chaparro, F., Salinas-Jimenez, J., & Smith, P. (1999). On the quality of ´ the data envelopment analysis model. Journal of the Operational Research Society, 50(6), 636–644.

• Prior, D. (2006). Efficiency and total quality management in health care organizations: A dynamic frontier approach. Annals of Operations Research, 145(1), 281–299.

• Regelson, M., & Fain, D. C. (2006). Predicting click-through rate using keyword clusters. Proceedings of the 2nd Workshop on Sponsored Search Auctions, Ann Arbor, MI: ACM New York.

• Ruggiero, J. (1998). A new approach for technical efficiency estimation in multiple output production. European Journal of Operational Research, 111(2), 369– 380.

• Ruggiero, J. (2003). Comment on estimating school efficiency. Economics of Education Review, 22(6), 631–634.

• Rusmevichientong, P., & Williamson, D. P. (2006). An adaptive algorithm for selecting profitable keywords for search-based advertising services. Proceedings of the 7th ACM Conference on Electronic Commerce, Ann Arbor, MI: ACM New York, 260–269.

• Rutz, O. J., & Bucklin, R. E. (2007). A model of individual keyword performance in paid search advertising, accessed June 5, 2012, available at SSRN: http://ssrn.com/abstract=1024765 or http://dx.doi.org/10.2139/ ssrn.1024765.

• Rutz, O. J., & Bucklin, R. E. (2011). From generic to branded: A model of spillover in paid search advertising. Journal of Marketing Research, 48(1), 87–102.

• Schiffman, S. S., Reynolds, M. L., & Young, F. W. (1981). Introduction to multidimensional scaling: Theory, methods, and applications (1st ed.). London, UK: Academic Press.

• Serrano-Cinca, C., Fuertes-Callen, Y., & Mar-Molinero, C. (2005). Measuring DEA efficiency in Internet companies. Decision Support Systems, 38(4), 557–573.

• Serrano-Cinca, C., & Mar-Molinero, C. (2004). Selecting DEA specifications and ranking units via PCA. The Journal of the Operational Research Society, 55(5), 521–528.

• Sherman, J. D., & Gold, F. (1985). Bank branch operating efficiency: Evaluation with data envelopment analysis. Journal of Banking and Finance, 9(2), 297– 315.

• Smith, P. (1997). Model misspecification in data envelopment analysis. Annals of Operations Research, 73(1), 233–252.

Ueda, T., & Hoshiai, Y. (1997). Application of principal component analysis for parsimonious summarization of DEA inputs and/or outputs. Journal of the Operations Research Society of Japan, 40(4), 466–478.

• Vassiloglou, M., & Giokas, D. (1990). A study of the relative efficiency of bank branches: An application of data envelopment analysis. The Journal of the Operational Research Society, 41(7), 591–597.
• Wasserman, T. (2011). Online ad revenues jump 23% to new record, accessed June 30, 2011, available at http://mashable.com/2011/05/ 26/q1-internet-advertising/.
• Weber, T. A., & Zheng, Z. (2007). A model of search intermediaries and paid referrals. Information Systems Research, 18(4), 414–436.
• Yang, S., & Ghose, A. (2010). Analyzing the relationship between organic and paid search advertising: Positive, negative or zero interdependence? Marketing Science, 29(4), 602–623.

Anteneh Ayanso is an associate professor of information systems at Brock University. He teaches undergraduate and graduate level courses in information systems/information technology. He received his PhD in information systems from the University of Connecticut and an MBA from Syracuse University. He is also certified in Production and Inventory Management (CPIM) by APICS. His research interests are in data management, business analytics, electronic commerce, and electronic government. His current related studies include topics such as search engine advertising, the role of social media technologies and applications in the commercial as well as public sector, and methods for profiling and measuring ICT positions and e-government readiness of world nations. He has published many articles in leading journals such as European Journal of Operational Research, Decision Support Systems, Journal of Database Management, Communications of the AIS, International Journal of Electronic Commerce, Journal of Computer Information Systems, Government Information Quarterly, AIS Transactions on Human-Computer Interaction, Information Technology for Development, and in proceedings of major international conferences in information systems and related fields. He currently serves as editorial review board member of the Journal of Database Management, International Journal of Convergence Computing, and International Journal of Electronic Commerce and regularly reviews articles for many leading journals in information systems and related fields.

Brian Mokaya received a Master of Science degree in management science from Brock University at St. Catharines, Canada. He is currently a senior SharePoint consultant at Ideaca Knowledge Services in Toronto, Canada. He completed his undergraduate degree in business and information technology from Strathmore University in Nairobi, Kenya. During his professional career, he has attained Microsoft technical specialist and Association for Information and Image Management certifications. His primary areas of interest lie in data mining, data analysis and business modeling, information and records management, and organizational change management.