Optimization Of Ads Allocation In Sponsored Search

ABSTRACT

We introduce the optimization problem of target-specific ads allocation. Technique for solving this problem for different target-constraints structures is presented. This technique allows us to find optimal ads allocation which maximize the target such as CT R, Revenue or other system performances subject to some linear constraints. We show that the optimal ads allocation depends on both the target and constraints variables.

Categories and Subject Descriptors

G.1.6 [Optimization]: Constrained optimization; H.3.5 [Online Information Services]: Commercial services; I.2.8 [Problem Solving, Control Methods, and Searche]: Control theory

Keywords

ads allocation, optimization, sponsored search, Theory, Algorithms

1. INTRODUCTION

Search engines use keyword auctions to get advertisers’ bids for ad allocation. Usually these auctions are implemented under the pay-per-click model in which an advertiser pays only for clicks on his ads.

Yandex display ads in two ways: the main part placed above the organic search results (the top-ad placement), and the rest on the right side (the right-ad placement). For the sake of brevity we consider the allocation problem only for the top-ad placement. The main question is how to allocate the ads given their attributes (i.e. bid, click-through rate, etc.) in order to optimize a target variable under some constraints on other variables. Here we introduce the mathematical model of the optimization problem and we present the technique for solving this type problems.

Researches about the computational advertisement describe a number of models of the ads allocation: the classical scheme to sort by CPM = bid·CT R, [1]; sort by bid^k ·CT R^l [2]; sort by rank = CT R·COEC·UCP ·bid under constraint rank > threshold (COEC is ‘clicks over expected clicks’ [4],

UCP – ‘the user click propensity’ [3]). But there are no any attempts to give an answer for the optimal ads allocation problem.

2. TARGET VARIABLES

There are three main participants: a search engine (SE), a user and advertisers. The SE wants to gain regularly as much money as it can. Hence it’s strictly necessary to be very popular among both Internet users and advertisers.

We use such measures as the click-through rate and the quantity of queries with sponsored results, aka commercial queries’ coverage. The last measure reflects the idea that amongst all users’ queries there is only some number with commercial intents. Under control of the ads quantity the click-through rate (CTR) can be viewed as a users’ feedback. Advertisers expect to get new customers from the Internet advertising campaign. For the sake of simplicity we use the CTR as the measure of the ad’s efficiency instead of the conversion rate.

We get three measures which are candidates for the target variable: the revenue of SE, the overall CTR and the commercial queries’ coverage.

3. OPTIMAL ALLOCATION PROBLEM

We assume that we have M users’ queries indexed by subscript j and N different banners indexed by subscript i. Then ti,j is a binary variable which equals one if the banner i are allocated for the query j else zero. Let T(t) = P i,j ti,j is a total amount of allocated banners, bidⁱ > 0 is an advertiser’s bid for the banner i and CT Ri,j ≥ 0 is an estimated click-through rate of the banner i for the query j (for unmatched (i, j) we put CT Ri,j = 0). Then we write formally our three measures as follow.

CTR(\mathbf{t}) = (\sum_{i,j} CTR_{i,j} \cdot t_{i,j}) / T(\mathbf{t}), \tag{1}

$revenue(\mathbf{t}) = \sum_{i,j} bid_i \cdot CTR_{i,j} \cdot t_{i,j},$ (2)

coverage(\mathbf{t}) = (\sum_{j} \mathbb{1}\{\sum_{i} t_{i,j} > 0\})/M. \tag{3}

Here in (2) we define the expected revenue of the SE in case the generalized first price auction, but in case the generalized second price auction we still use this measure in spite of it is always overestimate the true revenue. In (3) we use notation of the indicator-functions 1{·} for definition the number of queries with sponsored results.

There is one natural constraint – the number of possible slots for sponsored results is usually bounded above ( $\leq k$ ). This is written as follow.

\forall j \sum_{i} t_{i,j} \le k. \tag{4}

Now we can define the optimization problem in terms these notions and variables. For example, one of non-greedy SE’s choices of the target variable is the CTR. The rest measures can be used in the additional constraints:

$CTR(\mathbf{t}) \to \max_{\mathbf{t}}, \ s.t.$ (5)

$Revenue(\mathbf{t}) \ge R,$ (6)

$Coverage(\mathbf{t}) \le C.$ (7)

So we get the optimization problem (5) with constraints (4),(6),(7), where t is a NM-length vector with binary elements $t_{i,j}$ . It’s the discrete programming problem.

4. SKETCH OF THE SOLUTION

One of the main ideas of our solution is the relaxation of the origin discrete programming problem to a continues optimization problem. We replace the discrete $\mathbf{t}$ in (5),(4),(6),(7) with the continues analogue $\mathbf{t}$ such that $\forall i,j \ t_{i,j} \in [0,1]$ . This replacement is correct because of the optimal values are appeared to be either zero or one (except a few degenerate cases). In this case the solution of the continuous problem coincides with of the discrete one.

First of all we write the Lagrangian function which takes into account the revenue constraint (6).

$\mathcal{L}_1(\mathbf{t}) = CTR(\mathbf{t}) - \lambda_1(R - Revenue(\mathbf{t})) \to \max_{\mathbf{t}}.$ (8)

This problem will be a simple one if all terms in the right hand side of (8) are additive with respect to elements of $\mathbf{t}$ . The main difficulty is $CTR(\mathbf{t})$ nonlinearity. To solve this we add the auxiliary constraint $T(\mathbf{t}) = T_0$ and handle $T_0$ as additional variable. Then we get new Lagrangian:

$\mathcal{L}_{2}(\mathbf{t}) = \sum_{i,j} t_{i,j} (CTR_{i,j} \cdot T_{0}^{-1} + \lambda_{1}bid_{i} \cdot CTR_{i,j} - \lambda_{2}) + const \to \max.$ (5)

We have to solve this problem subject to (4),(7) and $\forall i,j \ t_{i,j} \in [0,1]$ . It’s clear that except some degenerate cases the optimal solution without (4),(7) is

$t_{i,j} = \mathbb{1}\{Score_{i,j} > 0\},$ (10)

where $Score_{i,j} = CTR_{i,j} \cdot T_0^{-1} + \lambda_1 bid_i \cdot CTR_{i,j} - \lambda_2$ .

To handle (4) it’s necessary to zero the least efficient $t_{i,j}$ (i.e. with the smallest $Score_{i,j}$ ) for j with $\sum_i t_{i,j} > k$ .

After this we can calculate the query’s score as $Q_j = \sum_i CTR_{i,j} \cdot T_0^{-1} + \lambda_1 bid_i \cdot CTR_{i,j} - \lambda_2$ and get optimal values for $t_{i,j}$ by means of excluding $t_{i,j}$ for j with $Q_j < \lambda_3$ . There is $\lambda_3 = \inf\{\lambda > 0 : \sum_j \mathbb{1}\{Q_j \geq \lambda\} \leq M \cdot C\}$ which manages (7).

Obviously the solution of (9) is a function of all auxiliary parameters: $\mathbf{t}^* = \mathbf{t}^*(\lambda_1, \lambda_2, \lambda_3, T_0)$ . We’ve shown the optimal value for $\lambda_3$ . The optimal value for $\lambda_2$ can be found from the equation $T(\mathbf{t}) = T_0$ . Then with fixed $\lambda_2, \lambda_3$ we find $T_0$ as $\max_{T_0} \mathcal{L}_1$ . Finally we find the optimal value for $\lambda_1$ from the constraint (6) according to the KKT theorem.

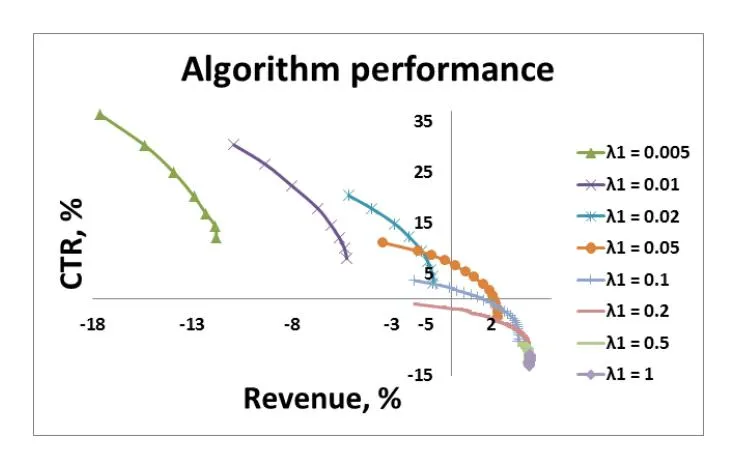
Figure 1: For each value $\lambda_1$ the (CTR, Revenue)-dependency is shown with respect to $\lambda_2$ . All measurements are calculated relative to the current Yandex algorithm’s performance.

5. CONCLUSIONS AND FUTURE WORK

In this short paper we introduced the mathematical optimization problem for the target-specific optimal ads allocation and presented the way of finding the solution.

Figure 1 shows that our algorithm outperforms the Yandex allocation algorithm in terms of the target variables.

Several heuristics for the computational complexity reduction for this algorithm coming soon in our next work. In our future work we want to include more complicated measures such as the conversion rate, the relevance or a quality score.

6. REFERENCES

• [1] Daniel C Fain and Jan O Pedersen. Sponsored search: A brief history. Bulletin of the American Society for Information Science and Technology, 32(2):12–13, 2006.
• [2] Sébastien Lahaie and David M Pennock. Revenue analysis of a family of ranking rules for keyword auctions. In Proceedings of the 8th ACM conference on Electronic commerce, pages 50–56. ACM, 2007.
• [3] Stefan Schroedl, Anand Kesari, and Leo Neumeyer. Personalized ad placement in web search. Proc. of ADKDD’10, 2010.
• [4] Wei Vivian Zhang and Rosie Jones. Comparing click logs and editorial labels for training query rewriting. In WWW 2007 Workshop on Query Log Analysis: Social And Technological Challenges, 2007.