Roi Constrained Optimal Online Allocation In Sponsored Search

Sponsored search plays a major role in the revenue contribution of e-commerce platforms. Advertising systems are designed to maximize platform revenue, but other goals also need to be considered, such as user experience, advertiser utility, and how to achieve the long-term revenue goal. A key component of a sponsored search system is online allocation, which makes real-time decisions to match users’ search requests with relevant ad campaigns to maximize platform revenue within constraints such as campaign budgets. Although much progress has been made, most of the research work on allocation problem has focused on satisfying guaranteed deals for display ads, and those challenges for allocation problems in sponsored search are not properly addressed. In this paper, we develop a framework to solve the large-scale sponsored search ad allocation problem, consisting of two main parts. One is an optimization problem solved offline by a parameter-server based architecture, and the other is an online strategy to alleviate the conflict with the auction mechanism during online service. Comprehensive offline evaluation on real production data and online A/B testing on real production system have been made. The experimental results demonstrate that through better allocating user queries to appropriate ads, the proposed model can significantly increase the platform’s revenue without sacrificing advertisers’ ROI.

Keywords Sponsored Search, Advertising systems, Online allocation, Auction mechanism

Sponsored search has always been an important part of e-commerce platform revenue generation. When a user issues a search query, search engines return the user organic search results along with sponsored ads on the same page. In this advertising system, platforms are incentivized to show ads that best match a user’s interests with advertiser’s bidding keywords, since platforms typically only get paid when a user clicks on an ad.

Advertising systems are designed to maximize platform revenue by displaying relevant ads, also obligated to balance other key performance indicators (KPI), such as user experience, advertiser utility, and long-term revenue goal. A typical sponsored search system is shown in Fig. 1. Advertisers first place an order on the platform by setting target ad-words, target user group attributes, and desired bid and budget settings. In the online service stage, a candidate ads list is determined according to the match with the user’s search request (such as search query matching ad-words, etc.), and the subsequent prediction module will estimate the clickthrough rate (pCTR) and the conversion rate (pCVR) of each ad. After that, an optional bid optimization module modifies the bid price to maximize platform revenue and other KPIs. Next, the online allocation module, which is the focus of this paper, sets the eligibility of each ad to participate in the auction according to the allocation model trained offline. Finally, the ads participating in the auction are sorted in descending order according to their estimated cost per mile (eCPM = pCTR $\times$ Bid) value under the generalized second price mechanism (GSP), and the top ranked k ads are displayed to the user. If an ad in position r is clicked, the advertiser will be charged with the bid price for ad in position r + 1.

One of the key components of the sponsored search advertising system is the online allocation module, which maximizes platform revenue by better matching users’ search requests with relevant advertising campaigns in real time, while subject to some additional business constraints, such as campaign budget constraints. Most of the previous studies on online allocation module are in the area of display advertising with guaranteed deals^1–5. Few studies have been done for sponsored search ads⁶. There are several reasons for this. First, sponsored search is performance-based and more performance-related constraints need to be considered, such like advertiser ROI constraints. Second, compared to the results of organic search, the results of sponsored search are less relevant to

¹School of Information and Electronic Engineering, Zhejiang University of Science and Technology, Hangzhou 310023, China. ²Alibaba Group, Beijing 100102, China. ³Zhejiang lab, Hangzhou 311121, China. ⁴Linyi Vocational University of Science and Technology, Linyi 276000, China. ⁵Mashang Consumer Finance Co., Ltd., Chongqin 401121, China. ⁶School of Computer Science and Technology, Hangzhou Dianzi University, Hangzhou 310023, China. ⁷Zhejiang Key Laboratory of Biomedical Intelligent Computing Technology, Hangzhou 310023, China. ⁸These two authors contributed equally. ^™email: zulong.czl@alibaba-inc.com

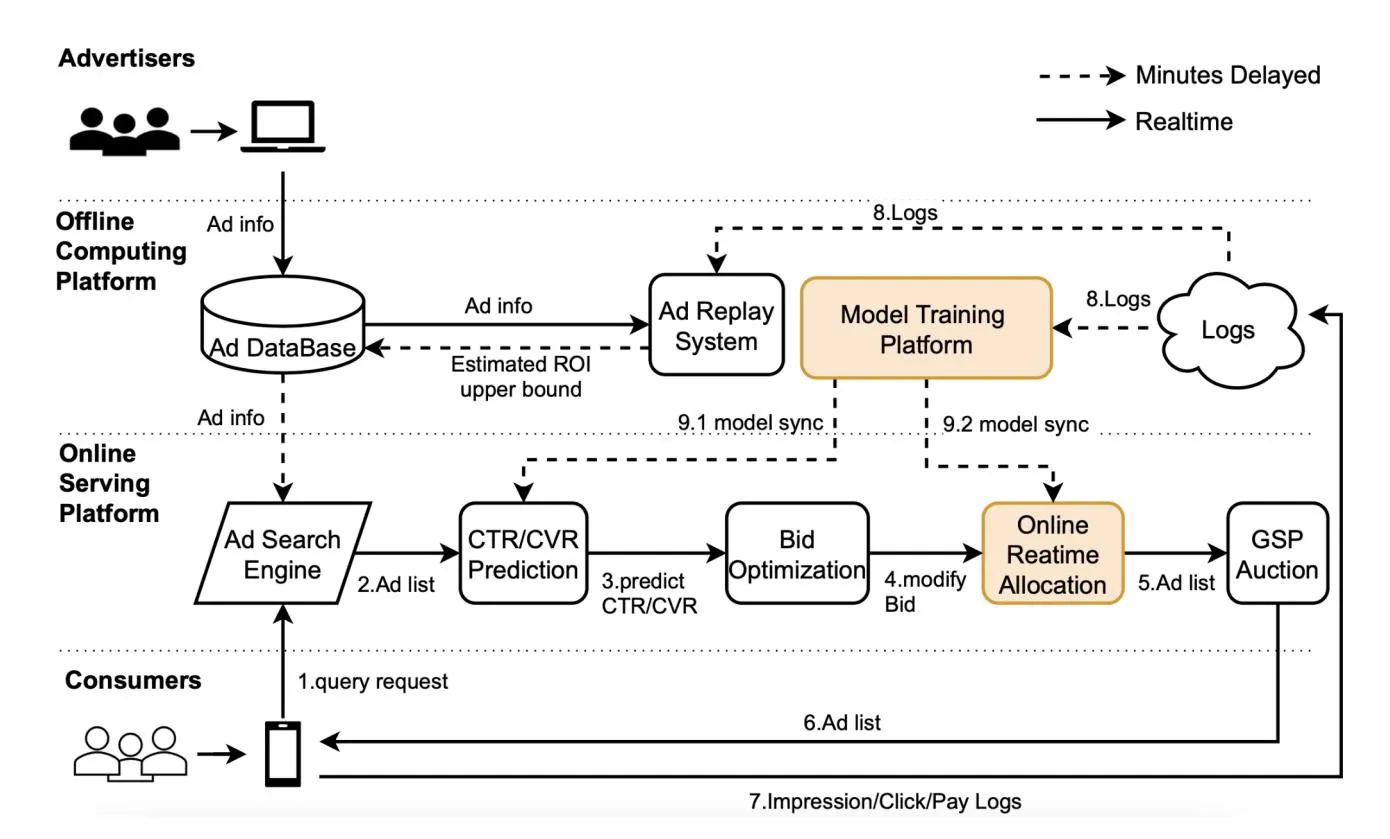
Fig. 1. A typical sponsored search system.

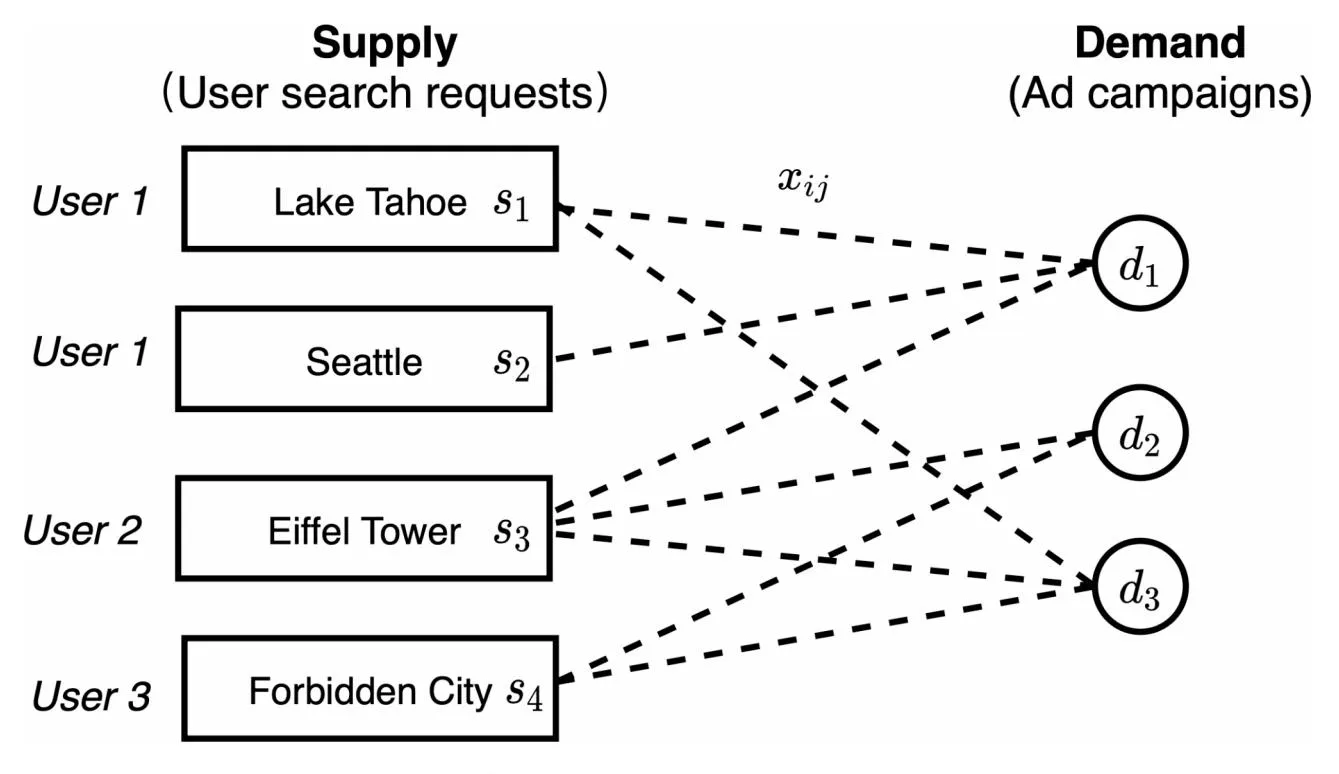
Fig. 2. Bipartite graph of supply and demand in sponsored search ad system.

Methods	Revenue	RPM	BCR	GMV	ROI
HWM	21259.32	53.31	13.33%	70015.95	3.2934
SHALE	23291.12	58.40	14.60%	83173.81	3.5692
AUAF	25901.58	64.95	16.24%	94950.61	3.6658
ODBC	49571.92	124.30	31.09%	173054.56	3.4910
OAM	40278.77	101.00	25.26%	135346.46	3.3597
ROAM	39444.78	98.91	24.73%	148571.29	3.7601

Table 1. Offline evaluation results (GMV is short for gross merchandise volume, GMV= $\sum_{i,j} s_i x_{ij} g_{ij}$ ).

users’ search intent. Therefore, in terms of user experience, the platform may benefit from limiting the number of the displayed search ads. Third, there is a conflict between allocation models and GSP auction mechanism that allocation models rank ads by allocation probability while the GSP auction ranks ads by eCPM. To this end, the allocation result may have no effect on the advertising systems.

In this paper, we formulate the sponsored search ads allocation problem as a constrained optimization problem. In addition to typical campaign budget constraints, we also consider advertiser ROI constraints, where the lower bound satisfies the advertiser’s goals and the upper bound ensures the stability of the advertising ecosystem. Since displaying too many ads will impact users’ search experience^7,8, in addition to platform revenue, we directly put maintaining a certain level of user experience as part of our target functionality.

Our new proposed model is called ROAM (ROI constrained Optimal Allocation Model). To solve it efficiently, a parallel optimization algorithm is developed based on the parameter server architecture, and generates a compact allocation plan for online serving. For the conflict between allocation model and GSP auction mechanism, an online strategy is designed. Comprehensive experiments have been conducted both offline and online on the real production data demonstrating that the proposed model can achieve significant improvements in both advertising platform’s revenue and advertiser’s ROI. The main contributions of our work are summarized as follows:

We propose a new allocation model that simultaneously optimizes platform revenue and user experience, and handles advertiser ROI constraints, one of the most important business constraints.
We develop a parallel optimization algorithm based on parameter server framework to solve ROAM efficiently, and design an online serving strategy that resolves the conflict between allocation model and GSP auction mechanism.
In online and offline experiments, our method improves revenue significantly compared to previous methods without sacrificing ROI. After more than three months from the first launch in production environment, our method is still running stably and works efficiently.

In this section, we conduct a brief survey on online allocation and sponsored search.

Online allocation

In online advertising area, allocation algorithms are used mainly for two different purposes: one for optimizing campaign (locally) and one for optimizing platform (globally).

When optimizing campaign, allocation algorithms are used to control the rate at which individual campaign’s budget is spent. Most commonly, for each search query, an allocation algorithm calculates the probability of serving each ad, and then applies throttling based on those probabilities^9–11.

When optimizing platform, allocation algorithm is typically formulated as a constrained optimization problem based on graph matching. Please refer to 12 for a detail and comprehensive survey. Chervonenkis et al. 13 find optimal ads allocation in sponsored search by relaxing the original integer programming to a continues optimization problem. Different approaches are proposed to deal with allocation problems with different objectives. For instance, Abrams et al. 14 formulate the allocation problem as a Linear Programming (LP) problem and applies column-generation method to solve it. However, it has limited scalability and can only be applied to high frequency queries. Zhang et al. 15 propose a consumption minimization model, in which the primary objective is to minimize the user traffic consumed to satisfy all advertisement contracts in online display advertising. Their method is based on finding the max flow solution for a bipartite graph matching problem. The authors in 6.16 reduce the number of variables of LP problem using the a primal-dual approach and obtain optimal solutions through offline simulations with historical data to maximize total revenue and other key performance of the auction based advertising subject to budget constraints. High Water Mark (HWM)¹ and SHALE² are both allocation models proposed for guaranteed display ads. They try to minimize under-delivery penalty as well as the gap between allocation probability and supply-demand ratio through iterative offline optimization method. The authors in 3,4,17 extend SHALE to address large scale allocation problem. In addition to guaranteed delivery, they also consider other types of real business needs, such as optimizing click-through rates, penalizing overallocation, and meeting frequency requirements.

Inspired by previous work above, we design a scalable allocation model for sponsored search. It combines two goals. One of them is to maximize advertising revenue and the other is to limit user experience degradation caused by displaying ads. Regarding constraints, it includes not only campaign budget constraint but also campaign ROI constraint.

The proposed methodology

The ad allocation problem is usually modeled as a bipartite graph matching problem with some constraints^2,17 as illustrated in Fig. 2. Let $G = (I \cup J, E)$ be a bipartite graph, where there are two types of nodes, i.e., the supply nodes $i \in I$ that represent user’s search requests belonging to a certain query type and the demand modes $j \in J$ that represent the ad campaigns. One supply node is connected with a demand node if the user’s search query matches the campaign’s target ad words and the user is in the campaign’s target user group. Each demand node j has a budget $d_j$ set by the advertisers and each supply node i has a weight $s_i$ indicating the number of user requests belonging to a certain query type.

Basic allocation problem formulation

The task of the allocation problem is to find the optimal allocation probability $x_{ij}$ , i.e., the fraction of the supply node i allocated to demand node j, that (1) maximizes some objective functions, and (2) satisfies some constraints. In this paper, we want to maximize the platform revenue with the minimum ads impressions to minimize the disruption to the organic search results. If one impression from supply node i is allocated to ad j on the demand side, the platform would charge the advertiser $c_{ij}$ and the advertiser would gain revenue from potential sales $g_{ij}$ , where $c_{ij} = pCTR_{ij} \times pCPC_{ij}$ and $g_{ij} = pCTR_{ij} \times pCVR_{ij} \times price_{j}$ . Note that, since $CPC_{ij}$ (Cost Per Click) is not available prior to GSP auction, we use average historical $CPC_{ij}$ of ad j as $pCPC_{ij}$ instead. The click-through rate $pCTR_{ij}$ and the conversion rate $pCVR_{ij}$ are generated from a separate predict model, $pCPC_{ij}$ is the cost per click charged to advertisers and $price_{j}$ is the price of the product/service sold by the advertiser. Considering these, the optimal allocation problem in sponsored search can be formally defined as:

$\max_{x} \sum_{i \in \Gamma(j), j} s_{i} x_{ij} c_{ij} - \lambda \sum_{i \in \Gamma(j), j} s_{i} x_{ij}^{2}$

$s.t. \sum_{i \in \Gamma(j), j} s_{i} x_{ij} c_{ij} \leq d_{j}, \forall j \text{ (budget constraint, 1a)}$

$\sum_{j \in \Gamma(j), j} x_{ij} \leq 1, \forall i \text{ (supply constraint, 1b)}$

$u_{j} \geq \frac{\sum_{i \in \Gamma(j)} s_{i} x_{ij} g_{ij}}{\sum_{i \in \Gamma(j)} s_{i} x_{ij} c_{ij}} \geq l_{j}, \forall j \text{ (ROI constraint, 1c)}$

$x_{ij} \geq 0, \forall i, j \text{ (non-negativity constraint, 1d)}$

where nodes in $\Gamma(j)$ are the neighbors of node j in the bipartite graph. The objective is to maximize the platform revenue $(s_ix_{ij}c_{ij})$ while minimizing the impressions allocated $(s_ix_{ij}^2)$ , i.e. minimizing the negative impacts to user experience. The hyper-parameter $\lambda$ balances the two aspects.

Constraints. Budget constraint (Eq. 1a): Each ad campaign has a budget $d_j$ set by the advertiser and the total cost of a campaign should not exceed its budget. Supply constraint (Eq. 1b): this should be obvious since the total

allocation from a supply node i should not exceed its capacity. ROI constraint ( $Eq.\ 1c$ ): the return over investment is defined as the ratio of the sales from the ads placed $\left(\sum_{i\in\Gamma(j)}s_ix_{ij}g_{ij}\right)$ over the cost charged to the campaign $\left(\sum_{i\in\Gamma(j)}s_ix_{ij}c_{ij}\right)$ . Usually, the advertisers set up a minimum ROI $l_j$ that we are obliged to guarantee, which implies the least sales revenue that the advertise can achieve with the budget invested. Furthermore, we set an upper limit on ROI for each campaign based on the historical data through a replay mechanism. On one hand, the upper limit of ROI is to ensure the stability of the ROI of advertisers, to prevent the ROI of advertisers from being very high when there is no competition, but falling a lot when the competition is fierce. The stability of ROI allows advertisers to make better marketing schedules in advance. On the other hand, the upper limit of ROI is set to reserve some high-quality traffic to improve the performance of ads with extremely low ROI, so as to avoid such advertisers churn on the platform.

Optimization algorithm

The allocation problem in Eq. (1) is an optimization problem with convex objective and linear constraints. We can obtain its optimal solution by solving its dual problem through the KKT condition. More specifically, the corresponding Lagrangian function is

$L(x, \alpha, \beta, \varphi, \eta, \zeta) = \sum_{i \in \Gamma(j), j} s_i x_{ij} c_{ij} - \lambda \sum_{i \in \Gamma(j), j} s_i x_{ij}^2 + \sum_j \alpha_j \left( \sum_{i \in \Gamma(j), j} s_i x_{ij} c_{ij} - d_j \right)$

$+ \sum_i \beta_i \left( s_i \sum_{j \in \Gamma(i)} x_{ij} - s_i \right) + \sum_j \eta_j \left( l_j \sum_{i \in \Gamma(j)} s_i x_{ij} c_{ij} - \sum_{i \in \Gamma(j)} s_i x_{ij} g_{ij} \right)$

$+ \sum_j \zeta_j \left( \sum_{i \in \Gamma(j)} s_i x_{ij} g_{ij} - u_j \sum_{i \in \Gamma(j)} s_i x_{ij} c_{ij} \right) - \sum_{i \in \Gamma(j), j} \varphi_{ij} x_{ij}$

$(2)$

From the KKT stationarity condition of $\frac{\partial L}{\partial x_{ij}} = 0$ and the complementary slackness for $\varnothing_{ij}$ , i.e., $\varnothing_{ij} = 0$ unless $x_{ij} = 0$ , we have:

$x_{ij} = \max\{0, \lambda c_{ij} - \alpha_{j}c_{ij} - \beta_{i} - \eta_{j}(l_{j}c_{ij} - g_{ij}) - \zeta_{j}(g_{ij} - u_{j}c_{ij})\}$ (3)

which is a function of $\alpha_j$ , $\eta_j$ and $\zeta_j$ , denoted by $x_{ij} = f(\alpha_j, \beta_i, \eta_j, \zeta_j)$ . The dual variables $\alpha$ , $\eta$ and $\zeta$ can be solved iteratively by coordinate descend or gradient descent algorithm until the objective function converges. The gradients of $\alpha$ , $\eta$ and $\zeta$ are calculated as:

$\frac{\partial L}{\partial \alpha_j} = \sum_{i \in \Gamma(j), j} s_i x_{ij} c_{ij} - d_j \tag{4}$

$\frac{\partial L}{\partial \eta_{i}} = l_{j} \sum_{i \in \Gamma(j)} s_{i} x_{ij} c_{ij} - \sum_{i \in \Gamma(j)} s_{i} x_{ij} g_{ij}$

$(5)$

$\frac{\partial L}{\partial \zeta_j} = \sum_{i \in \Gamma(j)} s_i x_{ij} g_{ij} - u_j \sum_{i \in \Gamma(j)} s_i x_{ij} c_{ij}$ (6)

Since the number of supply node is usually very large, we propose an efficient parallel algorithm to solve the allocation model using a Parameter-Server architecture, detailed in Algorithm 1. At first iteration, we calculate $\beta_i$ with zero as initial values of $\alpha_j, \eta_j, \zeta_j$ . After that, in each iteration on worker side, $beta_i$ is calculated with equation $\sum f\left(\alpha_j, \beta_i, \eta_j, \zeta_j\right) = 1$ , and $x_{ij}$ can be obtained with Eq. (3), then on server side $s_i x_{ij} c_{ij}$ , $s_i x_{ij} g_{ij}$ are gathered to update $\alpha_j, \eta_j, \zeta_j$ with Eq. (4) to Eq. (6). As shown in Algorithm 1, in the worker side, the time complexity is $O\left(\mid I\mid \ast \overset{\sim}{\Gamma}\right)$ , where $\overset{\sim}{\Gamma}$ is the average number of neighbors for each node in the bipartite graph. In the server side, the time complexity is $O\left(\mid J\mid\right)$ .

Algorithm 1 Offline Optimal Allocation Algorithm based on Parameter-Server Architecture
Input: Demand Side: d_i, u_i, l_i(\forall j); Supply Side: c_{ii,i \in \Gamma(i)}, g_{ii,i \in \Gamma(i)}(\forall ij \in E);
Output: the optimal dual values \alpha_i, \eta_i, \zeta_i, \forall j
1: While not converged do
2: >Worker:
3: for i \leftarrow 0 to |I| do
4:
                        Calculate \beta_i by solving Equation:
                                    \sum_{i\in\Gamma(i)} f(\alpha_i,\beta_i,\eta_i,\zeta_i) = 1;
5-
                        if \beta_i < 0 or no solution exists then
6:
7-
                                    update \beta_i = 0;
8:
                        end if
9:
                        for j \leftarrow 0 to |\Gamma(i)| do
10:
                                     Compute x_{ii} with Eq.(3);
11.
                        end for
12: end for
13:
            Push all s_i x_{ij} c_{ij}, s_i x_{ij} g_{ii} to Server;
14: ▶Server:
            Gather all s_i x_{ij} c_{ij}, s_i x_{ij} g_{ii} from Worker;
15:
16: for j \leftarrow 0 to |J| do
                        Update \alpha_i, \eta_i, \zeta_i with gradients Eq.(4) – Eq.(6);
17:
18: end for
19: Synchronize all \alpha_j, \eta_i, \zeta_i to Worker;
20: end while

Online serving

In the multiple representation learning framework, if the sub-networks are employed directly as in MMOE and PLE, the sub-networks would learn similar features that are very closely distributed in the representation space since they are fed with the same CTR labels. The worst case is that all the sub-networks collapse to the same space, which is harmful for dealing with sparse and long-tail data.

As shown in Algorithm 2, during the online service process, firstly, a set of candidate ads that best match user’s search request is selected. Then $\beta_i$ is solved for each request i with equation $\sum_{j\in\Gamma(i)}f\left(\alpha_j,\beta_i,\eta_j,\zeta_j\right)=1$ ( $\alpha_j,\eta_j,\zeta_j$ are solved in offline stage). After that, for each ad j in this list, allocation probability $x_{ij}$ can be computed by Eq. (3). Note that ad $j^*$ with highest $x_{ij}$ value among them may not be the winning ads in later auction process, because it may not have the highest eCPM value. However, to maximize platform’s revenue, which is proportional to the winning ad’s second price, we want ad $j^*$ to be always the winning ads in auction. To solve this conflict between allocation and GSP auction, our allocation algorithm put all ads whose eCPM is lower than the eCPM of ad $j^*$ , to be reserved to participate in the auction, as described in line 8 to line 19 of Algorithm 2.

Algorithm 2 Online Serving Algorithm

1: for each request i from online stream do
2: / ← Ø
            Calculate \beta_i by solving \sum_{j \in \Gamma(i)} f(\alpha_i, \beta_i, \eta_i, \zeta_i) = 1;
3.
4:
            if \beta_i < 0 or no solution exists then
5-
                         \beta_i \leftarrow 0
6.
7-
            Calculate all x_{ii} with Eq.(3);
            j^* \leftarrow argmax_{i \in \Gamma(i)} \{x_{ii}\};
9:
            if x_{ii} \le 0 then
10:
                         return Ø to auction;
11:
            end if
12:
            J \leftarrow J \cup j^*
            eCPM^* \leftarrow pCTR_{ij^*} * bid_{i^*};
13.
            for i \in \Gamma(i) do
14:
                         if pCTR_{ii} * bid_i < eCPM^* then
15:
16:
                                     I \leftarrow I \cup i;
                         end if
17:
18:
             end for
19:
            return / to participate in the auction;
20: end for

Experiments

In this section, we first describe some offline experimental results on logged production datasets. It includes comparison and analysis of the convergence properties and key performance of different models on these datasets and a sensitivity analysis of the hyperparameter values in our model ROAM. We also run an online A/B test to test our allocation model’s performance at runtime. We use a throttling-based algorithm as a baseline model. The results show that our model outperforms the baseline model in terms of both the platform’s RPM and the advertiser’s ROI.

Experimental setting

Data sets and evaluation metrics

We use a dataset with 1.2 million requests (supply node), 622 ad campaigns (demand nodes), and more than 4.8 million edges in the allocation bipartite graph created from sampling of logs dumped from production system. Note that the true click and conversion probability of each ad is still unknown even for offline model evaluation. We use model estimated CTR and CVR to represent the true values instead.

For the offline evaluation, we consider the following metrics:

• Budget Consumption Rate (BCR) is the ratio of total estimated revenue under allocation to total budget, and how close the offline evaluation result achieved by the methods to the upper bound can be observed by this metric. Budget consumption rate of offline evaluation is calculated as:

$BCR = \frac{\sum_{i \in \Gamma(j), j} x_{ij} c_{ij}}{\sum_{j} d_{j}}$

Revenue Per Mile (RPM) is a metric that represents how much money platform can earn per 1000 impressions. In our offline test context, the RPM evaluation is calculated as:

$RPM = 1000 * \frac{\sum_{i \in \Gamma(j),j} x_{ij} c_{ij}}{\sum_{i \in \Gamma(j),j} s_i x_{ij}}$

• Return on Investment (ROI) tries to directly measure the amount of return on advertiser’s displayed ads, relative to their advertising cost. In out offline test scenario, advertiser’s ROI is calculated as:

$ROI = \frac{\sum_{i \in \Gamma(j), j} x_{ij} g_{ij}}{\sum_{i \in \Gamma(j), j} x_{ij} c_{ij}}$

Benchmark methods

For offline allocation algorithm comparison, we compare the performance of our proposed method with four commonly used ones plus a variant version of ROAM, which has excluded the ROI constraint. To guarantee the fairness, we use the same objective function as described in our problem definition for all the methods.

HWM is proposed by¹. It first sorts all contracts in decreasing order of demand-supply ratio, then allocates each contract an equal portion from each eligible supply.
SHALE is proposed by², and it is modeled to minimize penalty and maximize representativeness, which is a measure of how close the allocation result is to demand-supply ratio.
AUAF is proposed by⁴. It is derived from SHALE with the main objective of maximizing the contract delivery rate. It also aims to maximize click through rate and avoid over-allocation.
ODBC is proposed by⁶, which formulates the allocation problem as a single objective linear programming problem to maximize revenue with the constraints of CTR and CVR in campaign level. One simplifying assumption made in this algorithm is that the distribution from which impressions are drawn is stationary, which means given sufficient historical data, optimal priori values of the dual variables can be learned by solving the dual offline.
OAM (ROAM without ROI constraint) is to demonstrate the effectiveness of ROI constraint in our proposed model. Specifically, the ROI constraint (i.e., Inequation 1c in problem definition) is removed from ROAM.

For models like HWM, SHALE and AUAF, demand-supply ratio is a key input to the representativeness objective. We have to first convert our ad campaign budgets demand to impressions demand, and calculate the demand-supply ratio, then we can apply these models to our allocation problem.

####Offline allocation evaluation

Comparison Results. We show the comparison results of different methods on five key performance indicators in Table 1. ODBC’s performance on all the indicators except ROI can be regarded as the upper bounds for other methods since it does not consider the ROI constraint. The proposed ROAM achieves the highest ROI while maintaining competitive Revenue, RPM, BCR and GMV.

Convergence Analysis. From Figs. 3, 4 and 5, we can see that all the comparison methods converge within 200 iterations on both BCR and RPM metrics. Note that, results for ODBC are shown as a horizontal line since it is solved by an open-sourced LP solver without the iteration procedures. HWM only runs through the data for only one round, hence it is also shown as a horizontal line. In fact, its performance equals that of SHALE after one iteration. The convergence results for ROI metric are shown in Fig. 5. The proposed ROAM achieves the best offline ROI metric and converges after 1000 iterations. Its ROI is much higher than OAM, indicating the importance of the ROI constraints. AUAF can converge fast after 100 iterations and achieves the second highest ROI. ROI of SHALE continues to increase with the iterations but is still far from ROAM after 1000 iterations. The offline ROI of ODBC is lower than ROAM, AUAF and SHALE. And HWM achieves the worst offline ROI.

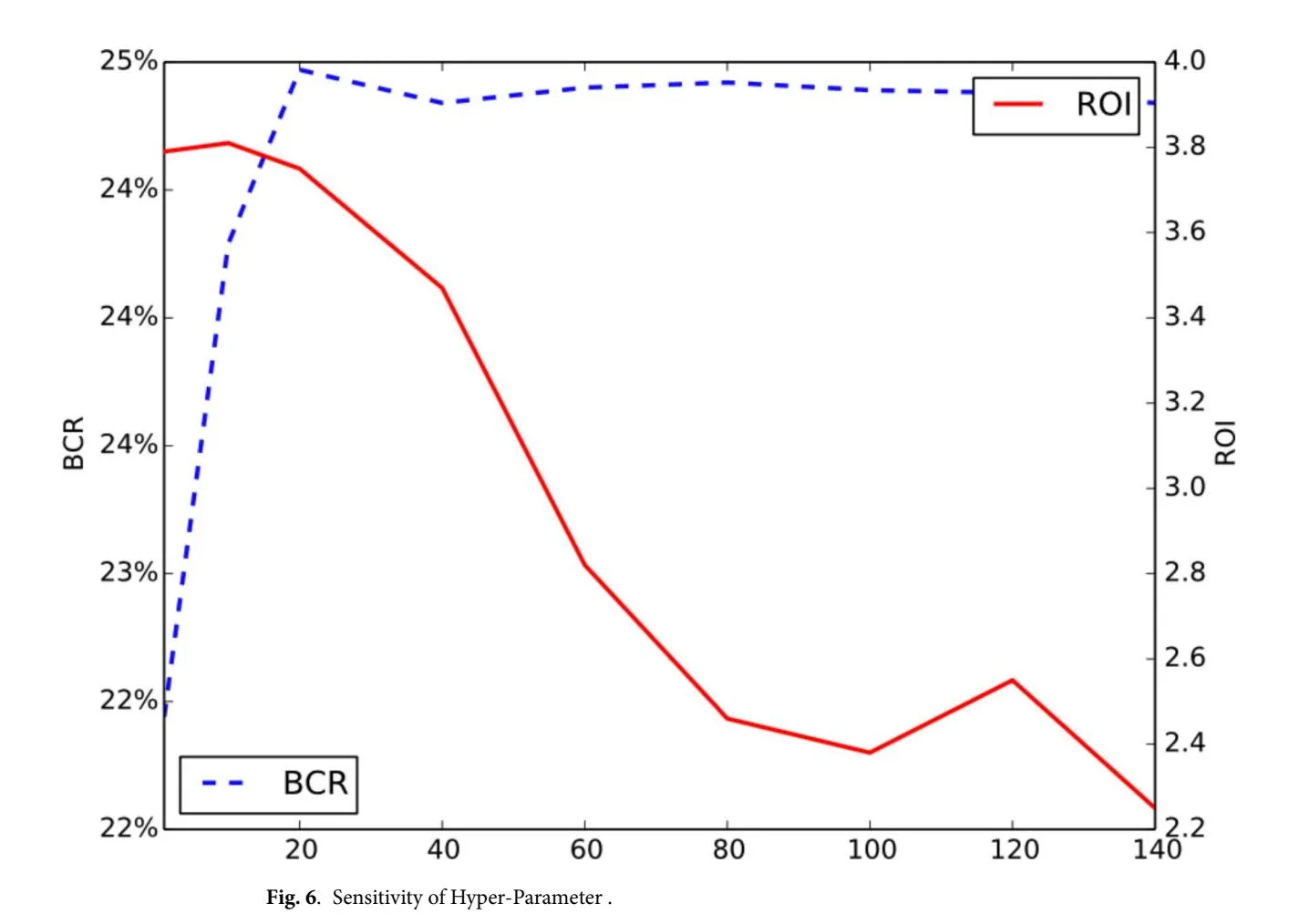
Hyper-Parameter Sensitivity Analysis. To conduct hyper-parameter sensitivity, we generate a synthetic dataset based on the dataset in³¹. According to our problem definition, larger lambda puts more weight on the revenue and ads will be displayed more times, disrupting user experience. As a result, CVR decreases with more ads shown, so does ROI since $ROI = \frac{pricesCVR}{bid}$ . Hence, is capable to balance ROI and revenue (or BCR). We evaluate the influence of hyper-parameter on ROAM in Fig. 6. The experimental optimal hyper-parameter = 20 is obtained by grid search.

Time Consumption Analysis. With millions of supply nodes and thousands of ad campaigns, our model takes less than 2 h to train for 1000 epochs with 1 server node (CPU) and 100 worker nodes (CPU). During the online serving stage, the serving time is negligible. The computation time is not a bottleneck.

To summarize, ODBC achieves the best revenue related metrics but with average performance on ROI. Best ROI is achieved by ROAM, followed by AUAF. AUAF is better than SHALE and HWM in terms of budget consumption rate and ROI. We will focus on the online performance of ODBC, ROAM and AUAF in the next section.

Online A/B testing

We conduct the online experiments to compare the proposed ROAM with AUAF, ODBC, and a baseline approach, which is a probabilistic throttling method that maximizes the conversion rate from visit to purchase (i.e., pCTR, pCVR) based on the consumption rate of the budget. Note that for a fair comparison, each comparison method gets an equal share of the budget of each ad campaign and trains their allocation model using their respective auction logs. If all the methods share the same pool of budget, methods that consume budget faster would grab budget from methods that consume budget slower, making the comparison unfair.

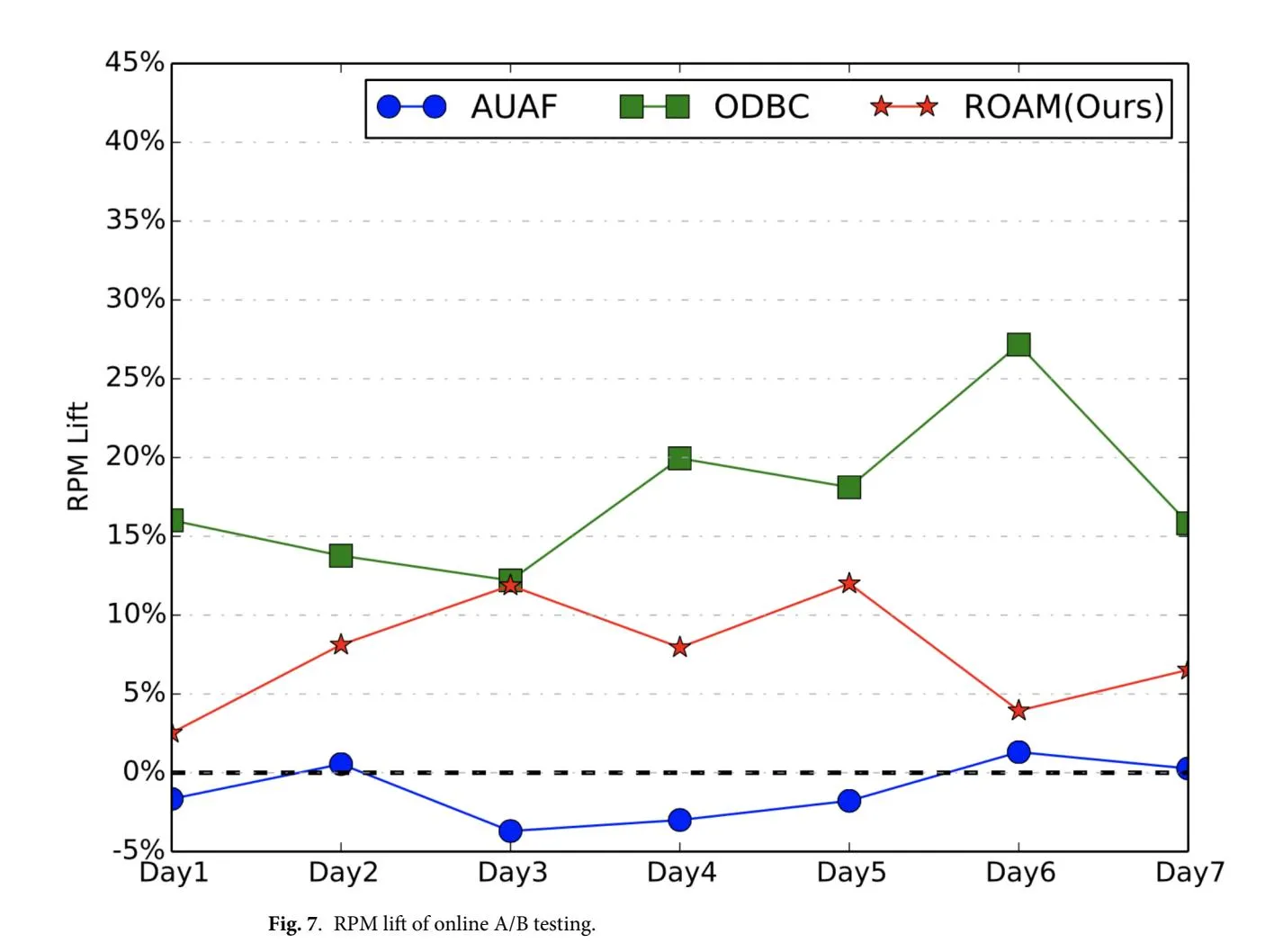
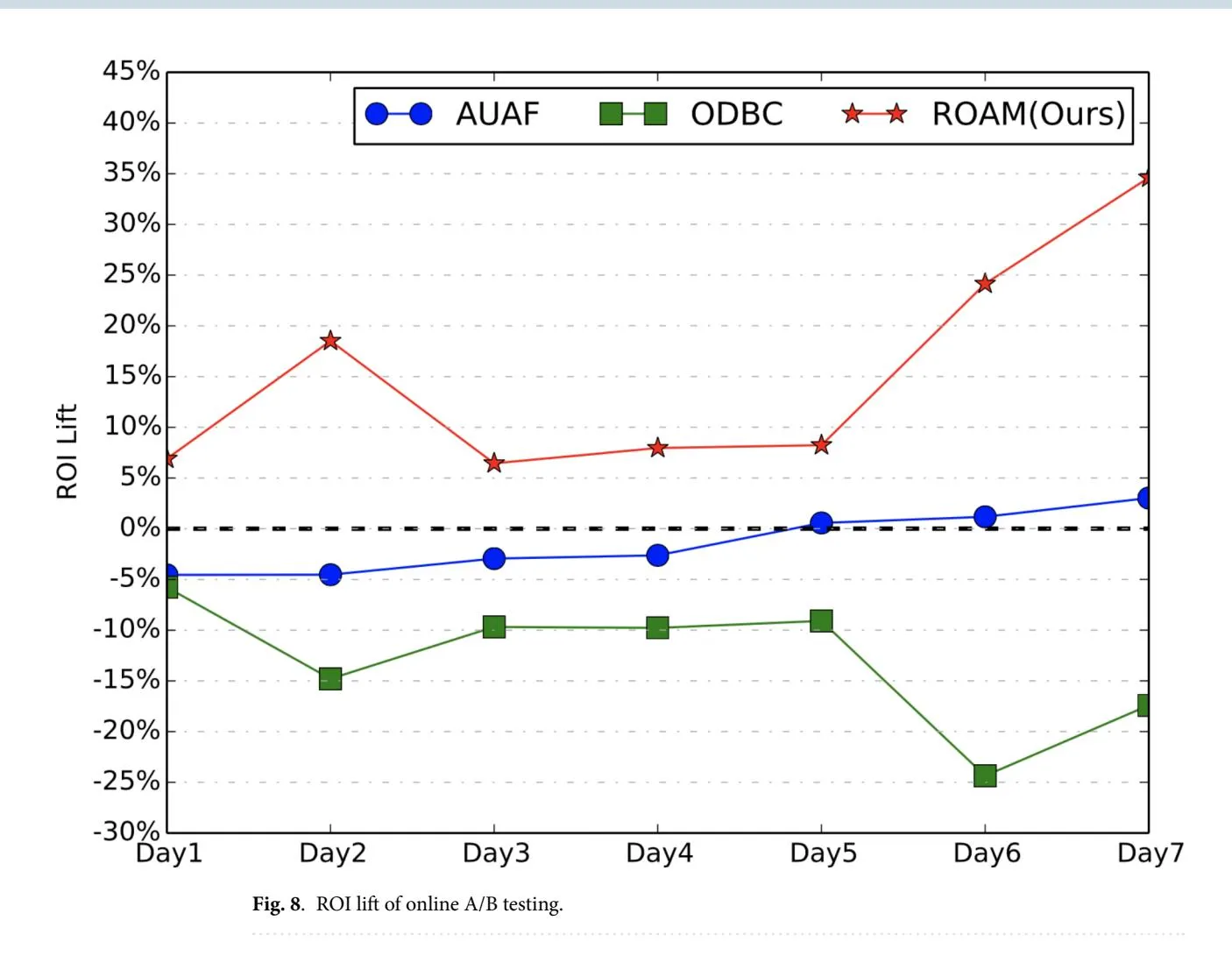
In online experiment, we focus on two metrics, i.e., RPM (with larger value indicating less user disturbance and higher effectiveness) and ROI. We conduct the online A/B testing for more than 7 days. Figures 7 and 8 show the results. Comparing to the probabilistic throttling-based baseline method, our proposed ROAM achieves stable and significant improvement on both on RPM and ROI. Especially, ROAM is the only method that achieves a positive lift on RPM without sacrificing ROI. Though ODBC has the highest RPM lift, it sacrifices a lot on ROI which is not acceptable. AUAF achieves no lift on both RPM and ROI.

It is worth mentioning that our model ROAM has been running stably in production for over three months since it was first launched.

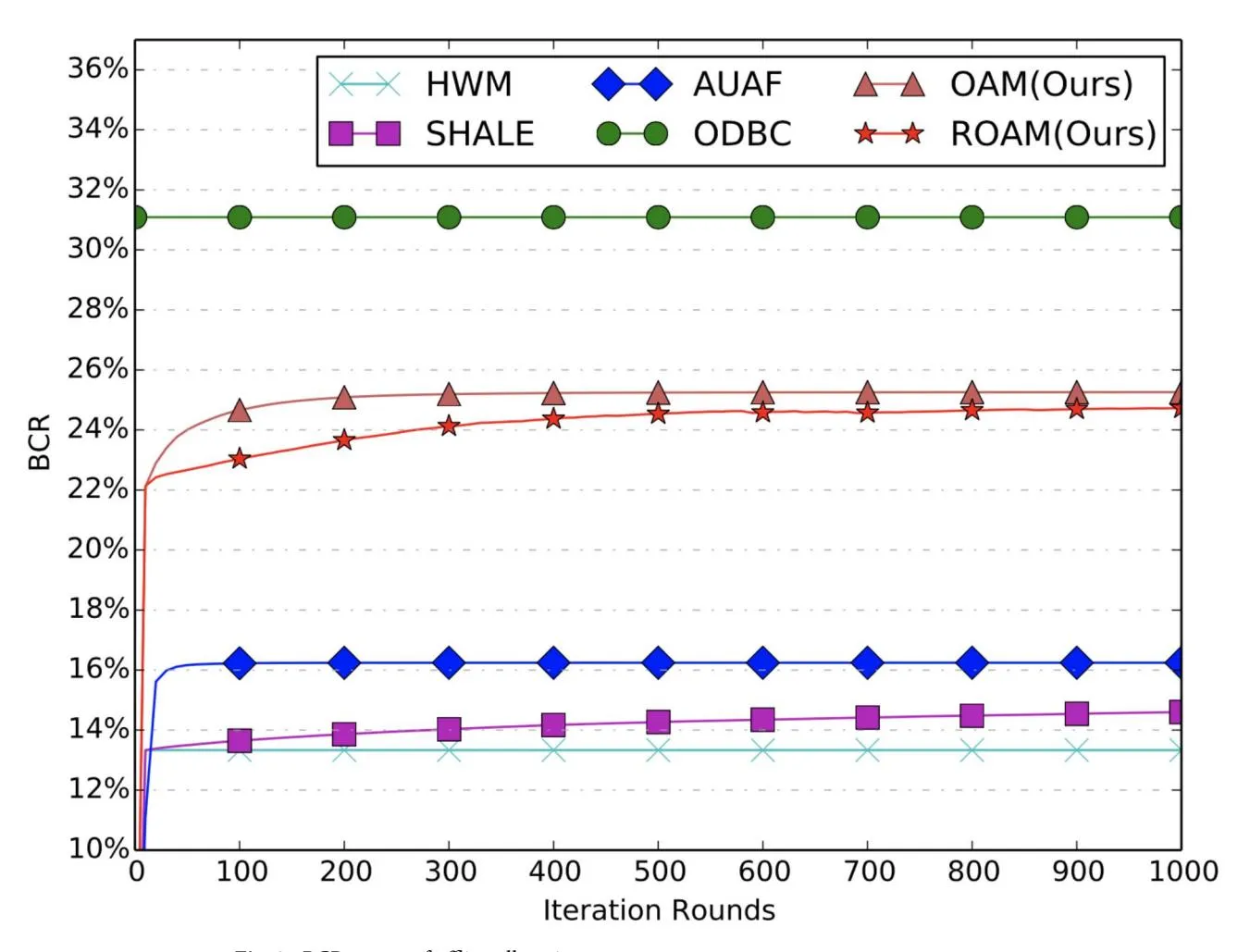
Fig. 3. BCR curves of offline allocation.

Conclusion

In this paper, we propose a new allocation model for sponsored search. It consists of two parts. For the offline part, an offline optimal solution is obtained by solving a constrained optimization problem from historical data with a quadratic objective and some linear constraints. It considers both platform revenue and user search experience in its goal, and makes a good trade-off between them by setting appropriate hyperparameter. An iterative algorithm is developed to efficiently solve this optimization problem in large scale. Instead of applying the offline solution directly online, we have designed some online strategies to address the potential conflict between the offline solution and GSP auction mechanism. Both offline and online experimental results show that our new model has made significant improvements on both platform revenue and advertiser ROI.

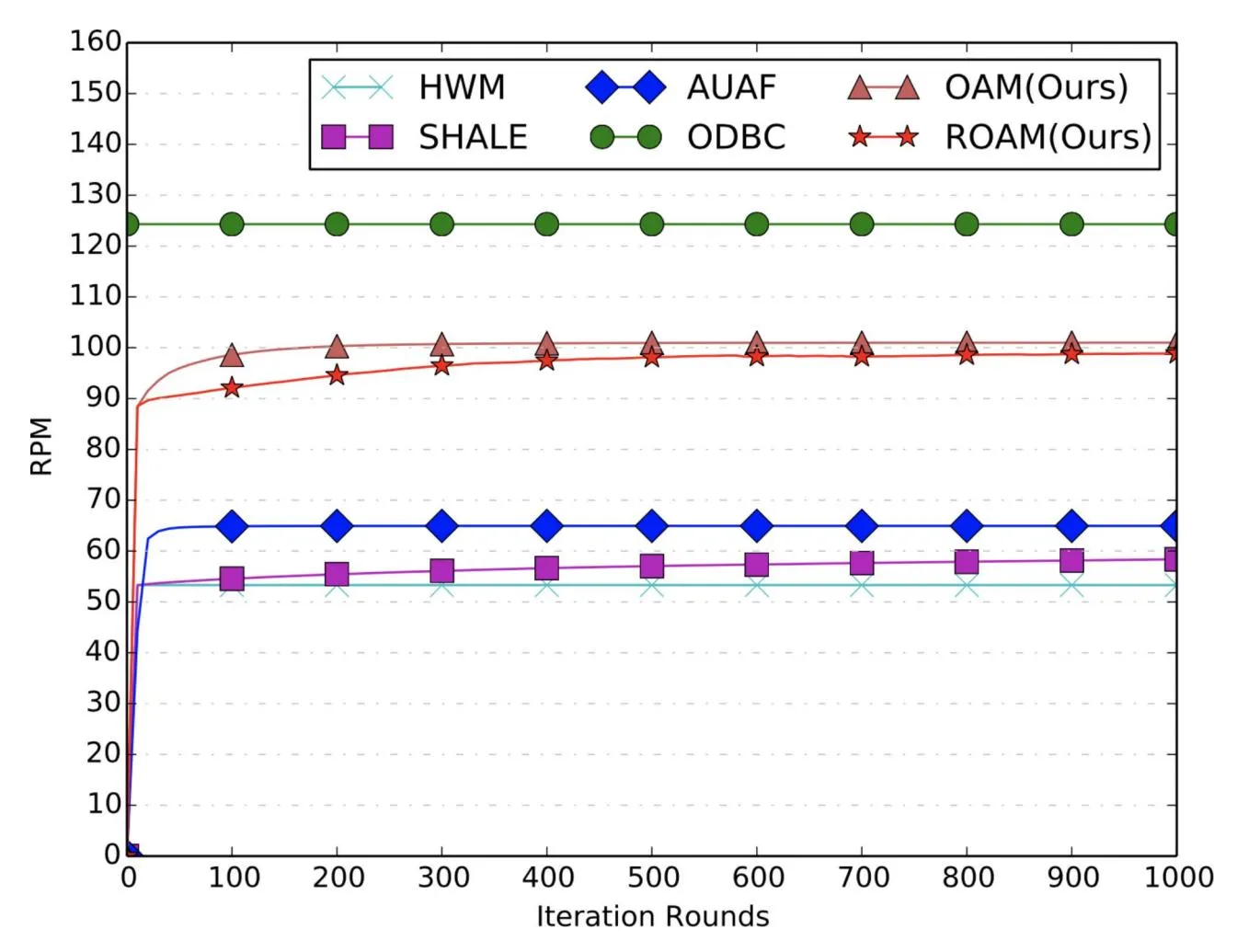
Fig. 4. RPM curves of offline allocation.

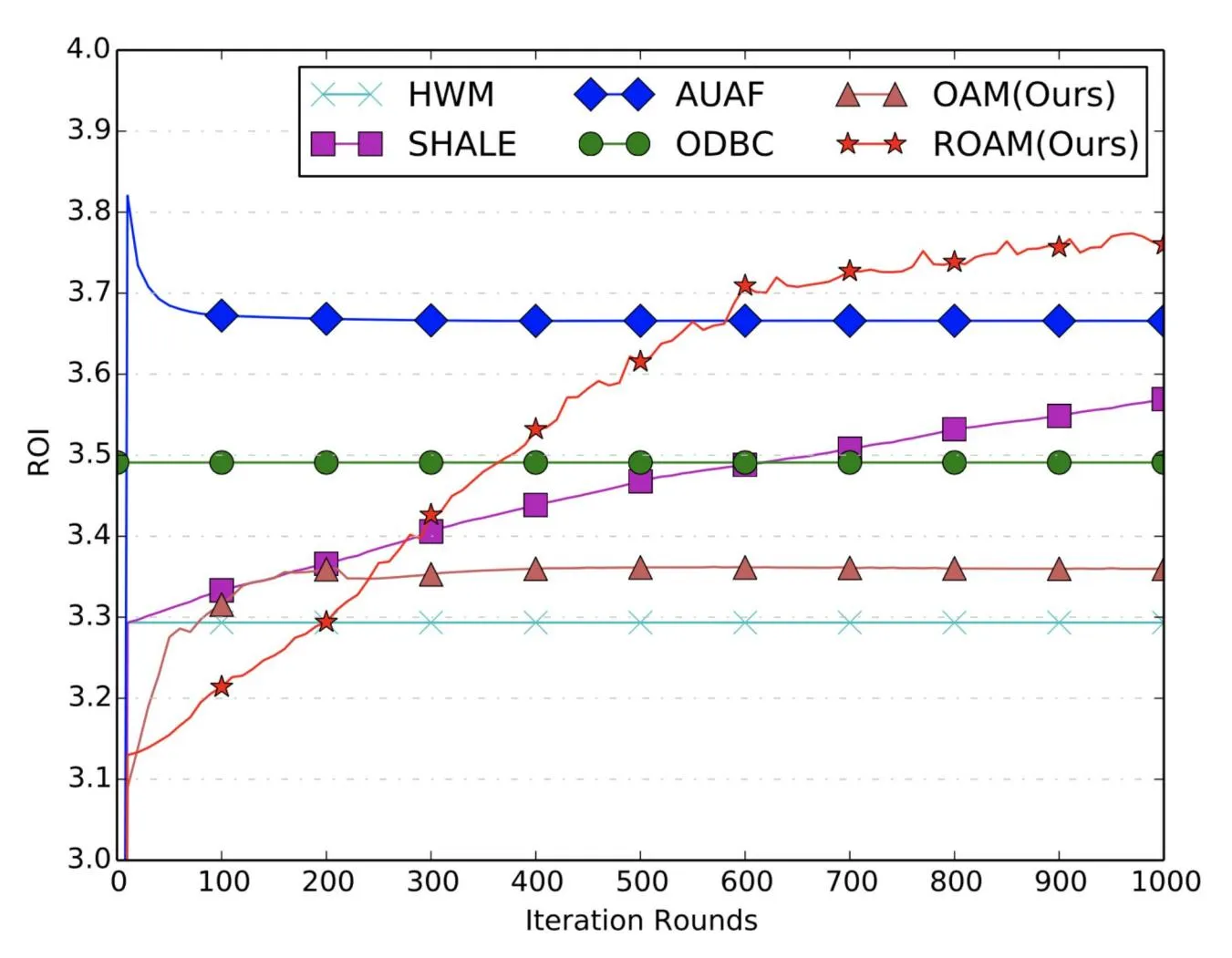
Fig. 5. ROI curves of offline allocation.

Data availability

The datasets used and/or analysed during the current study available from the corresponding author on reasonable request.

Received: 22 February 2024; Accepted: 23 October 2024

References

1. Chen, P. et al. Ad serving using a compact allocation plan, in Proceedings of the 13th ACM Conference on Electronic Commerce, pp. 319–336. (2012).
2. Bharadwaj, V. et al. Shale: An efficient algorithm for allocation of guaranteed display advertising, in Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, NY, USA: Association for Computing Machinery, pp. 1195–1203. [Online]. Available: (2012). https://doi.org/10.1145/2339530.2339718
3. Fang, Z. et al. Large- scale personalized delivery for guaranteed display advertising with real- time pacing, in 2019 IEEE International Conference on Data Mining (ICDM). IEEE, pp. 190–199. (2019).
4. Cheng, X. et al. An adaptive unified allocation framework for guaranteed display advertising, in ACM International Conference on Web Search and Data Mining, pp. 132–140, (2021).
5. Dai, L., Zu, Z., Wu, H., Wang, L. & Zheng, B. Fairness-aware guaranteed display advertising allocation under traffic cost constraint, in Proceedings of the ACM Web Conference 2023, pp. 3572–3580. (2023).
6. Wei, C. et al. Optimal delivery with budget constraint in e-commerce advertising, in 2nd Workshop on Online Recommender Systems and User Modeling. (eds. Vinagre, J., Jorge, A. M., Bifet, A., and Al-Ghossein, M.). PMLR, 46–58. (2019).
7. Goldstein, D. G., McAfee, R. P. & Suri, S. The cost of annoying ads, in Proceedings of the 22nd International Conference on World Wide Web, pp. 459–470. (2013).
8. Rafieian, O. Optimizing user engagement through adaptive ad sequencing. Mark. Sci.Bold”>42 (5), 910–933 (2023).
9. Karande, C., Mehta, A. & Srikant, R. Optimizing budget constrained spend in search advertising, in Proceedings of the sixth ACM international conference on Web search and data mining, pp. 697–706. (2013).
1. Agarwal, D., Ghosh, S., Wei, K. & You, S. Budget pacing for targeted online advertisements at linkedin, in Proceedings of the 20th ACM SIGKDD international conference on Knowledge discovery and data mining, pp. 1613–1619. (2014).
11. Xu, J., Lee, K., Li, W., Qi, H. & Lu, Q. Smart pacing for effective online ad campaign optimization, in Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp. 2217–2226. (2015).
12. Mehta, A. Online matching and ad allocation. Found. Trends Theoretical Comput. Sci. 8 (4), 265–368 (2013).
13. Chervonenkis, A., Sorokina, A. & Topinsky, V. A. Optimization of ads allocation in sponsored search, in Proceedings of the 22nd International Conference on World Wide Web, pp. 121–122. (2013).
14. Abrams, Z., Mendelevitch, O. & Tomlin, J. Optimal delivery of sponsored search advertisements subject to budget constraints, in Proceedings of the 8th ACM conference on Electronic commerce, pp. 272–278. (2007).
15. Zhang, J. et al. Efficient delivery policy to minimize user traffic consumption in guaranteed advertising, in Proceedings of the AAAI Conference on Artificial Intelligence, vol. 31, no. 1, (2017).
16. Chen, Y., Berkhin, P., Anderson, B. & Devanur, N. R. Real-time bidding algorithms for performance-based display ad allocation, in Proceedings of the 17th ACM SIGKDD international conference on Knowledge discovery and data mining, pp. 1307–1315. (2011).
17. Zhang, H. et al. A Request-Level Guaranteed Delivery Advertising Planning: Forecasting and Allocation, in Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp. 2980–2988, (2020).
18. Lian, Y. et al. Optimizing ad pruning of sponsored search with reinforcement learning, in Companion Proceedings of the Web Conference, 2021, pp. 123–127. (2021).
19. Li, Z., Wu, J., Sun, L. & Rong, T. Combinatorial keyword recommendations for sponsored search with deep reinforcement learning. arXiv Preprint arXiv:1907.08686, (2019).
20. Zhang, J. et al. Uni-retriever: Towards learning the unified embedding based retriever in bing sponsored search, in Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, pp. 4493–4501. (2022).
21. Li, F. et al. Graph intention network for click-through rate prediction in sponsored search, in Proceedings of the 42nd international ACM SIGIR conference on research and development in information retrieval, pp. 961–964. (2019).
1. Li, C. et al. Adsgnn: Behavior-graph augmented relevance modeling in sponsored search, in Proceedings of the 44th International ACM SIGIR Conference on Research and Development in Information Retrieval, pp. 223–232. (2021).
23. Zhu, J. et al. Textgnn: Improving text encoder via graph neural network in sponsored search, in Proceedings of the Web Conference 2021, pp. 2848–2857. (2021).
24. Tian, Z. et al. Pass: Personalized advertiser-aware sponsored search, in Proceedings of the 29th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, pp. 4924–4936. (2023).
25. Liu, H. et al. Cia-towards a unified marketing optimization framework for e-commerce sponsored search. arXiv Preprint arXiv:1806.05799, (2018).
26. Yang, X. et al. Aiads: Automated and intelligent advertising system for sponsored search, in Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, pp. 1881– 1890. (2019).
27. Zhao, W. et al. Personalized attraction enhanced sponsored search with multi-task learning, in Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, pp. 2632–2642. (2019).
28. Guan, Z. et al. Multi-agent cooperative bidding games for multi-objective optimization in e-commercial sponsored search, in Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining, pp. 2899–2909. (2021).
29. Ou, W. et al. A survey on bid optimization in real-time bidding display advertising. ACM Trans. Knowl. Discovery Data. 18 (3), 1–31 (2023).
30. Li, M. Dynamic reserve price design for lazada sponsored search, arXiv preprint arXiv:2206.10295, (2022).
31. Kong, L. et al. LOVF: Layered Organic View Fusion for Click-through Rate Prediction in Online Advertising, in Proceedings of 46th International ACM SIGIR Conference on Research and Development in Information Retrieval, pp. 2139–2143. (2023).