Triangular Bidword Generation For Sponsored Search Auction

ABSTRACT

Sponsored search auction is a crucial component of modern search engines. It requires a set of candidate bidwords that advertisers can place bids on. Existing methods generate bidwords from search queries or advertisement content. However, they suffer from the data noise in <query, bidword> and <advertisement, bidword> pairs. In this paper, we propose a triangular bidword generation model (TRIDENT), which takes the high-quality data of paired <query, advertisement> as a supervision signal to indirectly guide the bidword generation process. Our proposed model is simple yet effective: by using bidword as the bridge between search query and advertisement, the generation of search query, advertisement and bidword can be jointly learned in the triangular training framework. This alleviates the problem that the training data of bidword may be noisy. Experimental results, including automatic and human evaluations, show that our proposed TRIDENT can generate relevant and diverse bidwords for both search queries and advertisements. Our evaluation on online real data validates the effectiveness of the TRIDENT’s generated bidwords for product search.

KEYWORDS

sponsored search, advertising bidword generation, query expansion, triangle training, Information systems→Sponsored search advertising;• Computing methodologies → Natural language generation.

1 INTRODUCTION

Sponsored search auction is an indispensable part of commercial search engine, which aims to recommend appropriate advertisements to search users. Sponsored search auction is also called bidword auction, as it takes bidwords as bridges between search query

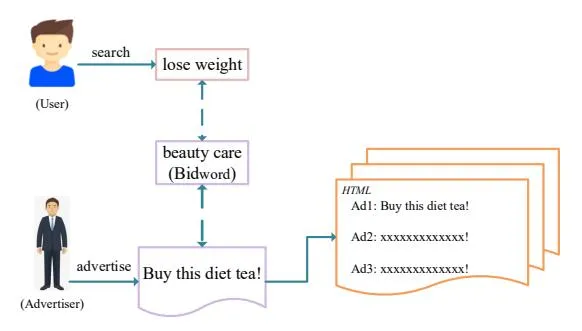
Figure 1: An illustration of sponsored search auction system. Here “lose weight” is the search query from user, and “beauty care” is the bidword purchased by advertiser.

and advertisements [2, 26], which is widely adopted in online advertising by search companies. Specifically, a search engine first retrieves a set of advertisements whose associated bidwords match a user issued query. It then ranks these advertising candidates according to an auction process by considering both the quality and the bid price of each advertisement [2, 26]. Finally, the topranked advertisements will be presented in the search page. For example, in Figure 1, advertisers bid a so-called bidword for their product in the auction system, and the so-called bidword is also associated with a search query according to some match methods. Thus, when a user delivers this query in the search engine, the advertisement of this product will be triggered and inserted into the result search page. Obviously, the so-called bidword plays an important role in sponsored search for connecting advertising (Ad) and query. Therefore, generating relevant and diverse bidwords for Ad and query are crucial, as it can improve the effectiveness and efficiency of advertising-bidword auction and query-bidword matching. Through this way, high-quality bidwords can bring great revenues for sponsored search [1, 19, 23, 26, 48].

Generating satisfactory bidwords is non-trivial for sponsored search. Traditional methods are mainly matching-based, which match the co-occurrence words between existed bidwords [5] and search query [14] (or advertisement [5]). Different matching strategies have been used, including exact match [17], broad match [10] and phrase match [15, 28]. However, bidwords of Ads or queries belonging to a rare domain are hard to obtain using matching strategies, because there are barely overlapped words between these Ads (or queries) and existing bidwords. Additionally, matching-based methods cannot recommend novel bidwords that do not exist in the search history.

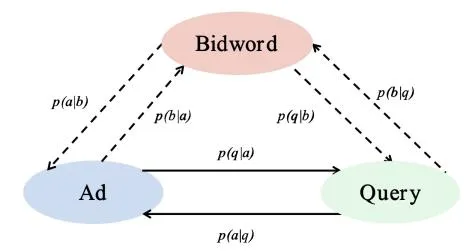
Figure 2: The architecture of the triangular bidword generation model (TRIDENT). The solid lines mean the data of the direction is extensive and high-quality, while the dash lines mean the data of the direction is noisy. a, q and b denote Ad, query and bidword, respectively.

Recently, deep learning approaches give effective alternatives for bidword generation, which could address the concerns of matching-based methods. Given paired data such as <query, bidword> and <advertisement, bidword>, we can employ the sequence to sequence model with encoder-decoder framework from neural machine translation [3, 6, 41] to directly generate bidwords from search queries or advertisements [16]. The sequence to sequence (Seq2Seq) model has been widely used and obtains gains in applications of modern search engine, such as advertising keyword suggestion [16], query keyword generation [26] and query expansion [23].

However, current approaches of directly applying Seq2Seq in bidword generation do not achieve enough gains, due to the fact that the training data may be noisy. Specifically, high-quality training data of paired <query, bidword> or <advertisement, bidword> are hard to obtain, which is caused by the common keyword bidding problem¹. Thus, noises are introduced into <query, bidword> or <advertisement, bidword> data, and noisy training data may prevent Seq2Seq from generating high-quality bidwords. Fortunately, the paired data of <query, advertisement> are quite easy to obtain from the user-clicks of search engine, which are always high-quality. How to fully exploit <query, advertisement> data for bidword generation is still under explored.

In this paper, we propose a TRIangular biDword gENeratTion model (TRIDENT), which can effectively leverage the high-quality data of paired <query, advertisement> to generate more relevant and diverse bidwords for both advertisements and queries. Motivated by the research of low-resource neural machine translation [8, 11, 12, 34], our proposed TRIDENT is simple yet effective, the intuition of which is very straightforward: $P(\text{query} \mid \text{Ad})$ can be well learned by high-quality <query, advertisement> data, and they could also be estimated as Figure 2 using the Maximum Marginal Likelihood [22]: $\tilde{P}(\text{query}|\text{Ad}) = \sum_{\text{bidword}} P(\text{bidword}|\text{Ad}) P(\text{query}|\text{bidword})$ . Finally, P(bidword|Ad) can be indirectly supervised in the triangle by minimizing the divergence between P(query|Ad) and $\tilde{P}(\text{query}|\text{Ad})$ . P(bidword|query) could be learned in the same way. Thus, information of high-quality <query, advertisement> data can also be used to generate bidwords, alleviating the

problem that <query, bidword> and <advertisement, bidword> may be noisy.

Experimental results with both automatic and human evaluations show that bidwords generated by our TRIDENT are significantly better than baselines in both relevance and diversity. The model performance can be further improved by using the proposed constrained beam search.

Our contributions are listed as follows:

• We propose TRIDENT, a novel triangular indirectly supervised bidword generation model, which can effectively boost the performance of bidword generation by exploiting high-quality <query, advertisement> data as an indirect supervision signal.
• Experimental results with both automatic and human evaluations demonstrate that our model can generate relevant and diverse bidwords for both advertisements and queries.
• To our best knowledge, TRIDENT is the first work to employ a triangular training framework for bidword generation.

2 BACKGROUND

2.1 Notation

In the following formulations, we use A,Q and B to denote Ad, query and bidword, respectively. Suppose < a,q> is a pair of high-quality < Ad, query> data, we denote the < Ad, query> dataset as $D_{aq}=\{< a,q>_i\}_{i=i}^N$ and N is size of $D_{aq}$ . Likewise, $D_{ab}=\{< a,b>_i\}_{i=1}^M$ and $D_{qb}=\{< q,b>_i\}_{i=1}^L$ can be denoted for the < Ad, bidword> and < query, bidword> datasets in the same way.

2.2 Encoder-Decoder Framework

The encoder-decoder framework is a widely used generative neural network architecture, which is first introduced in Neural Machine Translation [6, 41]. Here we implement our method based on Transformer [42] encoder-decoder framework. The encoder first transforms the input sequence $X = \{x_1, x_2, ..., x_n\}$ into a sequence of feature vectors $Z = \{z_1, z_2, ..., z_n\}$ , from which the decoder generates an output sequence $Y = \{y_1, y_2, ..., y_m\}$ . The encoder and decoder are trained jointly to maximize the conditional probability of Y given X:

$P(Y|X) = \sum_{j=1}^{m} \log P(y_j | y_{< j}, X; \theta)$ (1)

Specifically, Transformer consists of stacked encoder and decoder layers. The encoder layer is a self-attention block followed by a position-wise feed-forward block, based on which the decoder layer has an extra encoder-decoder attention block. For self-attention and encoder-decoder attention, a multi-head attention block is used to obtain information from different representation subspaces at different positions. Each head corresponds to a scaled dot-product attention, which operates on query Q, key K and value V:

Attention(Q, K, V) = softmax( $\frac{QK^T}{\sqrt{d_k}}$ )V (2)

where $d_k$ is the dimension of the key. Then the heads are concatenated and once again projected, resulting in the final values, as

^&lt;sup>1Keyword bidding problem: Advertisers are preferable to bid on more popular bidwords to improve the trigger probability of their Ads even if those bidwords are not relevant with their products.

described in the following formulation:

\begin{aligned} \text{MultiHead}(Q, K, V) &= \text{Concat}(\text{head}_1, ..., \text{head}_h) W^O \\ \text{head}_i &= \text{Attention}(QW_i^Q, KW_i^K, VW_i^V) \end{aligned} \tag{3}

where $W_i^Q$ , $W_i^K$ , $W_i^V$ and $W^O$ are trainable parameters, and h is the number of heads.

3 PROPOSED METHOD: TRIDENT

In this section, we describe our proposed triangular bidword generation model TRIDENT, which is able to generate relevant and diverse bidwords for both Ads and queries. The overall architecture is shown in Figure 2.

Generally TRIDENT includes six generation processes. It first starts with modeling the generation task $A\Rightarrow Q$ on the high-quality < A, Q> data, leading to a generation probability P(q|a) for each < a, q> pair. Then we decompose $A\Rightarrow Q$ into two phases by training another two generation models $A\Rightarrow B$ and $B\Rightarrow Q$ on the noisy data pairs (< A, B> and < Q, B>). By taking B as an intermediate latent variable, we can calculate another generation probability $\tilde{P}(q|a)$ . Then our model will be trained to eliminate the divergence between the direct probability P(q|a) and the indirect one $\tilde{P}(q|a)$ . Through this way, P(b|a) can be indirectly supervised in the triangular architecture among A, Q and B. The situation is similar by reversing the direction of $A\Rightarrow Q$ , and thus the quality of generated bidwords with noisy data can be improved.

In the following subsections, we will first introduce the training of the triangular architecture. Then we describe how to construct bidword as an intermediate latent variable. Next, we will discuss more training details and present our algorithm in the form of pseudo code. Finally, a constrained beam search is proposed to further improve the diversity of the bidwords.

3.1 Triangular Model Training

Since it is difficult to obtain high-quality < A, B > and < Q, B > data, we propose a triangular architecture (TRIDENT) to promote bidword generation with the help of high-quality < A, Q > data.

Overall, there are six generation models among Ad, query and bidword in the proposed TRIDENT, as depicted in Figure 2. These models all employ the Transformer encoder-decoder framework, and are jointly trained through the following training objective:

L = \lambda L_{MLE} + (1 - \lambda)L_{TRI} \tag{4}

where $\lambda$ is a hyper-parameter to govern the relative importance of the two losses, $L_{MLE}$ is the likelihood loss of generation models on the noisy data (<A, B> and <Q, B>), and $L_{TRI}$ is the divergence between the direct generation probability on <A, Q> data and the indirect one computed by taking B as an intermediate latent variable in the triangle.

Specifically, $L_{MLE}$ can be computed as:

$L_{MLE} = -\sum_{\langle a,b \rangle \in D_{ab}} [P(a|b;\theta_{ba}) + P(b|a;\theta_{ab})]$

$-\sum_{\langle q,b \rangle \in D_{ab}} [P(q|b;\theta_{bq}) + P(b|q;\theta_{qb})]$ (5)

where $P(b|a;\theta_{ab})$ is the conditional probability of a bidword b given an Ad a, $\theta_{ab}$ is the corresponding parameters, and so on. All

the probabilities are calculated using Equation1 with their corresponding parameters $\theta$ . Through $L_{TRI}$ , we aim to minimize the cross-entropy of direct generation probability on <A, Q> and the indirect one:

\begin{split} L_{TRI} &= -\sum_{\langle a,q \rangle \in D_{aq}} \left[ P(q|a;\theta_{aq}) \, \log \tilde{P}(q|a;\theta_{ab},\theta_{bq}) \right. \\ &\left. + P(a|q;\theta_{qa}) \, \log \tilde{P}(a|q;\theta_{qb},\theta_{ba}) \right] \end{split} \tag{6}

Here $\tilde{P}(q|a;\theta_{ab},\theta_{bq})$ and $\tilde{P}(a|q;\theta_{qb},\theta_{ba})$ are the indirect probabilities between A and Q, which are computed by taking B as an intermediate variable:

$\tilde{P}(q|a;\theta_{ab},\theta_{bq}) = \sum_{b} P(q|b;\theta_{bq})P(b|a;\theta_{ab})$

$\tilde{P}(a|q;\theta_{qb},\theta_{ba}) = \sum_{b} P(a|b;\theta_{ba})P(b|q;\theta_{qb})$ (7)

In detail, TRIDENT first directly train two generation models between A and Q, after which these two models are frozen and will indirectly supervise the subsequent bidword generation process by regarding B as a bridge connecting A and Q. Instead of training two separated generation models, we build the bi-directional dependencies between A and Q simultaneously. Inspired by previous works on dialogue systems [24, 37], we propose to maximize the mutual information A between A and A to model their bi-directional dependencies. To simplify computation, we maximize the following lower bound of mutual information between A and A:

\begin{split} I(A,Q) &= \frac{1}{2} \Big[ \sum_{\langle a,q \rangle} P(a,q) \log \frac{P(a,q)}{P(a)} - \sum_{\langle a,q \rangle} P(a,q) \log P(q) \Big] \\ &+ \frac{1}{2} \Big[ \sum_{\langle a,q \rangle} P(a,q) \log \frac{P(a,q)}{P(q)} - \sum_{\langle a,q \rangle} P(a,q) \log P(a) \Big] \\ &\geq \frac{1}{2} \Big[ \sum_{\langle a,q \rangle} P(a,q) \log P(q|a) + \sum_{\langle a,q \rangle} P(a,q) \log P(a|q) \Big] \end{split}

Suppose A and Q are both sampled from a uniform distribution and thus the above lower bound can be reformulated as:

$I(A,Q) \ge \alpha \left[ \sum_{q} P(q|a) \log P(q|a) + \sum_{a} P(a|q) \log P(a|q) \right]$

$\iff \sum_{\langle a,q \rangle \in \mathcal{D}_{A}, a} P(q|a) \log P(q|a) + P(a|q) \log P(a|q)$ (9)

where $\alpha$ denotes the sampling probability from a uniform distribution.

Through maximizing the above objective, we get two generation models $P(q|a;\theta_{aq})$ and $P(a|q;\theta_{qa})$ . These two models will indirectly supervise the subsequent bidword generation process as described in $L_{TRI}$ . In this way, bidword generation performance can be improved even if noisy data are used.

3.2 Bidword as the Bridge between Query and

After constructing the generation model $A \Rightarrow Q$ , it can indirectly supervise the generation process $A \Rightarrow B$ and $B \Rightarrow Q$ by taking B

$^{^2} Available\ at\ http://en.wikipedia.org/wiki/Mutual\_information/$

as a bridge to connect A and Q. Given an <a, q> pair, our TRIDENT regards B as an intermediate latent variable as follows:

\tilde{P}(q|a;\theta_{ab},\theta_{bq}) = \sum_{b} P(q|b;\theta_{bq}) P(b|a;\theta_{ab}) \tag{10}

Thus, $\tilde{P}(q|a; \theta_{ab}, \theta_{bq})$ can be obtained by enumerating all possible b that is relevant with both a and q.

However, it is difficult to enumerate all possible candidates, as the search space is exponential to the size of vocabulary and the length of b is unknown. Instead, we leverage two approaches to compute $\tilde{P}(q|a;\theta_{ab},\theta_{bq})$ : one is calculating an average vector space to represent the intermediate bidword variable [22] (denoted as TRIDENT-A), the other is based on sampling method [20] (denoted as TRIDENT-S).

Specifically, TRIDENT-A calculates a sequence of expected word embedding to represent the intermediate bidword variable. Given an input a, the expected word embedding at each decoding step means the weighted average vector of all possible words:

$\tilde{b_j} = \sum_{w \in V} P(w|w_{< j}, a; \theta_{ab}) Emb(w)$ (11)

where $j=1,2,...,T_b$ and $T_b$ is a given length of b.V is the vocabulary and we enumerate each possible word w in V.Emb(w) is the word embedding of w, and $P(w|w_{< j},a;\theta_{ab})$ is the weight which is the prediction probability for w at j-th step. Thus, a sequence $\tilde{b}=\{\tilde{b_1},\tilde{b_2},...,\tilde{b_{T_b}}\}$ is obtained, which will be subsequently taken as input by model $B\Rightarrow Q$ to predict q:

\tilde{P}(q|a;\theta_{ab},\theta_{bq}) = P(q|\tilde{b};\theta_{bq}) \tag{12}

Alternatively, TRIDENT-S computes $\tilde{P}(q|a;\theta_{ab},\theta_{bq})$ through a sampling method as follows:

$\tilde{P}(q|a;\theta_{ab},\theta_{bq}) = \sum_{b \in C} P(q|b;\theta_{bq}) P(b|a;\theta_{ab})$ (13)

C is the candidate set, each of which is sampled from $P(b|a;\theta_{ab})$ . The sample size is set to 5 in our experiments. To make the loss differentiable, Gumbel-Softmax [18] is used here.

Likewise, $P(a|q; \theta_{ab}, \theta_{ba})$ can be calculated in the same way.

3.3 Training Details

Overall, we first train the models P(a|q) and P(q|a) between A and Q based on a lower bound of their mutual information. Then taking B as a bridge to connect A and Q, $\tilde{P}(a|q)$ and $\tilde{P}(q|a)$ can be computed through another four generation models (P(a|b), P(b|q), P(q|b)) and P(b|a). Subsequently, the cross-entropy between P and $\tilde{P}$ is minimized, and through this way, P(b|a) and P(b|q) can be indirectly supervised in the triangle. Thus, the quality of generated bidwords can be improved. The detailed training process is summarized in Algorithm1.

3.4 Constrained Beam Search

Li et al. [25] find that most responses in the N-best candidates produced by the traditional beam search are similar. To solve this problem, we propose a constrained beam search to foster diversity in the generated bidwords. We force the head words of N-candidates should be different, and then the model continues to generate a response by a greedy decoding strategy after such head words

Algorithm 1 Training TRIDENT

Input: A high-quality dataset $D_{aq} = \{ \langle a, q \rangle_i \}_{i=1}^N$ for A and Q; A noisy dataset $D_{ab} = \{ \langle a, b \rangle_i \}_{i=1}^M$ for A and B; A noisy dataset $D_{qb} = \{ \langle q, b \rangle_i \}_{i=1}^L$ for Q and B; Learning rate n:

Output: Parameters $\theta_{aq}$ , $\theta_{qa}$ , $\theta_{ab}$ , $\theta_{ba}$ , $\theta_{qb}$ and $\theta_{bq}$

• 1: repeat
• 2: sample a batch $B_{aq}$ of $\langle a, q \rangle$ pairs from $D_{aq}$
• 3: compute the gradient of the lower bound of mutual information defined in Equation 9: $g = \nabla I(B_{aq}; \theta_{aq}, \theta_{qa})$
• 4: update parameters $\theta_{aq}$ and $\theta_{qa}$ : $\theta = \theta + \eta * g$
• 5: until convergence
• 6: repeat
• 7: sample a batch $B_{aq}$ of $\langle a, q \rangle$ pairs from $D_{aq}$ , $B_{ab}$ of $\langle a, b \rangle$ pairs from $D_{ab}$ and $B_{qb}$ of $\langle q, b \rangle$ pairs from $D_{qb}$
• s: compute the gradient on loss L in Equation 4: $g = \nabla L(B_{aq}, B_{ab}, B_{qb}; \theta_{ab}, \theta_{ba}, \theta_{qb}, \theta_{bq})$
• update parameters $\theta_{ab}$ , $\theta_{ba}$ , $\theta_{qb}$ , $\theta_{bq}$ : $\theta = \theta \eta * g$
• 10: until convergence

Datase	et	Size	Vocabulary	Average Length
(A., Q.)	A.	12, 998, 127	119, 806	16.22
(A., Q.)	Q.	14, 634, 482	477, 684	4.67
(A., B.)	A.	188, 773	28, 113	18.71
	B.	7, 338, 854	188, 629	4.09
(Q., B.)	Q.	11, 913, 539	316, 243	4.62
	B.	2, 540, 295	103, 346	2.86

Table 1: The detailed statistics of the datasets. A., Q. and B. denote Ad, query and bidword, respectively.

are determined. Through such a simple method, our model can generate the N-best candidates with more diversity, which have great potential to bring extra revenues for sponsored search.

4 EXPERIMENT

In this section, we conduct extensive experiments to show the performance of the proposed TRIDENT in generating reasonable bidwords for sponsored search.

4.1 Dataset

Since there are no off-the-shelf datasets for triangular bidword generation, we build the datasets by ourselves. Three forms of data pairs are collected from a commercial search engine, which are <Ad, query> data, <Ad, bidword> data and <query, bidword> data, respectively. Each item of <Ad, query> data represents a user click combined with a user issued query. Each item of <Ad, bidword> data is an Ad and a related bidword purchased by the advertiser. Each item of <query, bidword> data is a user issued query and a bidword purchased by the advertiser whose Ad is shown in the search page. The detailed statistics of the three data pairs are shown in Table 1. We randomly sample 5,000 pairs of each form as validation and test set.

Models		Relevance		Diversity
		Conv-KNRM	BLEU	Self-BLEU	distinct-3	distinct-4
	TF-IDF Method	0.503	0.063	0.700	0.119	0.153
Match Models	Mean Pooling Method	0.548	0.098	0.679	0.147	0.209
	Max Pooling Method	0.548	0.109	0.673	0.147	0.209
Neural Models	Transformer_base	0.634	0.133	0.403	0.166	0.252
	MT-A2B	0.657	0.149	0.483	0.153	0.236
Our Models	TRIDENT-S	0.753	0.151	0.362	0.168	0.279
	TRIDENT-A	0.781	0.185	0.284	0.218	0.296

Table 2: Conv-KNRM, BLEU, Self-BLEU and distinct-3/4 results for advertising (Ad) bidword generation.

Models		Relevance		Diversity
		Conv-KNRM	BLEU	Self-BLEU	distinct-3	distinct-4
	TF-IDF Method	0.614	0.104	0.698	0.208	0.273
Match Models	Mean Pooling Method	0.637	0.135	0.739	0.215	0.297
	Max Pooling Method	0.651	0.156	0.729	0.239	0.336
Neural Models	Transformer_base	0.783	0.186	0.404	0.258	0.387
	Attn-Q2B	0.801	0.209	0.517	0.243	0.358
Our Models	TRIDENT-S	0.853	0.205	0.352	0.286	0.397
	TRIDENT-A	0.896	0.239	0.269	0.381	0.454

Table 3: Conv-KNRM, BLEU, Self-BLEU and distinct-3/4 results for query bidword generation.

4.2 Experimental Settings

We implement our proposed model with PyTorch³. Spercifically, our TRIDENT is trained using configuration $transformer\_base$ [42], which contains a 6-layer encoder and 6-layer decoder with 512-dimensional hidden representations. All the training data are first tokenized using the tokenizer provided by Chang et al. [4], and then the words are split with a subword vocabulary learnt by BPE [36]. The size of the constrained beam search is set to 32. We tune the hyper-parameter $\lambda$ from 0.1 to 1.0 with step 0.1, and find that $\lambda = 0.6$ achieves the minimum perplexity on the validation set.

We apply Adam algorithm [21] as the optimizer with a linear warm-up over the first 4000 steps and linear decay for later steps. The batch size and learning rate are set to 32 and 1e-4, respectively. The proposed model is trained for 100,000 steps on 8 Nvidia Telsa V100-32GB GPUs.

4.3 Baseline Models

We compare our proposed models against the following representative baselines, including matching based methods and neural network models:

• (1) Matching based methods first convert an Ad/query into a feature vector, and then computes its relevance score with other Ads/queries by applying the cosine similarity function on their feature vectors. The bidword whose paired Ad/query achieves the highest similarity score is taken as the retrieved one. Three matching based methods are adopted:

  • TF-IDF Method [32] represents each Ad/query as a term tf-idf value vector.

• Max Pooling Method [44] represents each Ad/query as the max pooling of Glove word vectors [31].

• Mean Pooing Method [46] represents each Ad/query as the mean pooling of Glove word vectors [31].

(2) The following Neural Network Models are also taken as strong baselines:

• Transformer_base: We implement the transformer_base model as described in [42] with the constrained beam search.
• Attn-Q2B: We reimplement Google’s attention-based bidword generation model for query [9].
• MT-A2B: The Ad-bidword generation model using multitask learning [45] is also reimplemented.

4.4 Automatic Evaluation

• 4.4.1 Metrics. The following automatic metrics are used to evaluate the performance of the proposed model:
  • Conv-KNRM: Conv-KNRM [7] models n-gram soft matches for ad-hoc search. Previous works have validated that Conv-KNRM can, to a large extent, capture the semantic-level similarity between queries and documents. Conv-KNRM here is trained on the <Ad, query> dataset, in which the click rate is taken as the similarity score.
  • BLEU Score: BLEU [30] is a popular metric that calculates the word-overlap score of the generated bidwords against gold-standard ones.
  • Self-BLEU: Self-BLEU is a metric to evaluate the diversity of the generated bidwords [49]. Regarding one bidword as hypothesis and the others as references, we calculate its

^&lt;sup>3Available at https://pytorch.org/

Models	Relevance	Diversity	Fluency
Match Models	A. to B.	1.38	1.80	1.97
Match Models	Q. to B.	1.29	1.34	1.92
Transformer base	A. to B.	1.64	1.36	1.94
Transformer_base	Q. to B.	1.64	1.63	1.72
Neural Models	MT-A2B	1.42	1.73	1.96
Neurai Models	Attn-Q2B	1.65	1.25	1.86
TRIDENT-A	A. to B.	1.76	1.84	1.95
I KIDEN I-A	Q. to B.	1.70	1.64	1.80

Table 4: The results of human evaluation. A., Q. and B. denote Ad, query and bidword, respectively. A. to B. and Q. to B. represent bidwords generated from Ad and query, respectively.

BLEU score [30]. Finally, Self-BLEU is the average BLEU score of all candidates.

• Distinct: Distinct-1/2/3/4 is the proportion of the distinct uni-grams/bi-grams/tri-grams/four-grams in all the generated tokens [24]. Here we report the distinct-3/4 results, which are more contrastive. Distinct metrics can be used to evaluate the diversity of the generated bidwords.

4.4.2 Results. The bidword generation results from advertising and query are reported in Table 2 and Table 3, respectively. As shown in the two Tables, our model (TRIDENT-A) outperforms the competitors in all cases.

Notably, the bidwords generated by our models are significantly better than baselines in both relevance and diversity whether from advertising or query. In Table 2, MT-A2B performs best among all baselines in relevance, while our proposed TRIDENT-A exceeds it on Conv-KNRM with a fairly significant margin of 0.124 points. Moreover, our TRIDENT-A is also superior to MT-A2B on BLEU score with a significant boost about 3.6 points. The similar results can be observed in the Table 3. It demonstrates that our TRIDENT are capable of generating more relevant bidwords than other neural models. The reason is that the triangular architecture built in TRIDENT can exploit the high-quality <Ad, query> data to improve the performance of the noisy data (<query, bidword> and <Ad, bidword> data). Additionally, our TRIDENT-A and Transformer base significantly outperform other models in diversity. The Self-BLEU scores achieved by our TRIDENT-A/S and Transformer base are much lower than other models in both Table 2 and Table 3. This makes sense because generative models can generate novel bidwords that do not exist in the training corpus and the proposed constrained beam search can further promote the diversity. Besides, we also observe that TRIDENT-A performs better than TRIDENT-S in all cases, demonstrating that the expected word embedding method works better than sampling method.

4.5 Human Evaluation

4.5.1 Evaluation Settings. We conduct a human evaluation to better understand the quality of the bidwords generated by our triangular architecture. In this way, we can decide if these bidwords are suitable to be recommended to advertisers.

Specifically, 50 Ads and 50 queries are first randomly sampled from the test set of <Ad, bidword> and <query, bidword> data. All neural models and max pooling method, which performs best among all matching based methods, are selected as baselines to compare with our proposed TRIDENT-A. For each of the Ads and queries, all models generate the corresponding bidwords with beam size 32. Later the pairs of <Ad, top-32 bidwords> and <query, top-32 bidwords> are presented to five human annotators with order disrupted. Then they evaluate the produced bidwords at relevance, fluency and diversity levels all by 3-scale rating (0, 1, 2). A higher score means a better performance. Relevance assesses whether the bidwords are coherent and meaningful for an Ad or query. Fluency tests the general grammar correctness. Diversity decides if the top-32 bidwords are diverse.

Agreements to measure inter-rater consistency among the annotators are calculated with the Fleiss’s kappa [13]. As a result, the Fleiss’s kappa for relevance, fluency and diversity is 0.857, 0.912 and 0.803 respectively, all of which indicate “substantial agreement”.

4.5.2 Results. The human evaluation results are reported in Table 4. It shows that TRIDENT-A achieves the highest scores in both relevance and diversity (2-tailed sign test, p value < 0.05).

As we can see, TRIDENT-A outperforms MT-A2B/Attn-Q2B in relevance with a significant margin of 0.34/0.05 points. Besides, TRIDENT-A also achieves higher scores than Transformer_base in relevance. These observations indicate that our proposed TRIDENT-A is capable of generating more relevant bidwords than other neural models. Our interpretation is that some extra information can be leveraged through the triangular architecture, which can provide an indirect supervision for bidword generation. Moreover, the diversity scores of TRIDENT-A are also higher than baselines, indicating that a better bidword generation model can be obtained through the triangular framework and the proposed constrained beam search can further promote the diversity. Notably, the max pooling method performs best in fluency. It is easy to understand as matching based methods directly select bidwords from the corpus, which generally have no grammar errors.

4.6 Additional Analysis

We further investigate the influence of the used <Ad, query> data size and the proposed constrained beam search.

4.6.1 Effect of the <Ad, Query> Data Size. In order to investigate the influence of the high-quality <Ad, query> data size, we test the performance of our TRIDENT-A with different <Ad, query> data size.

The performance curve with different <Ad, query> data size is shown in Figure 3. Specifically, the TRIDENT-A achieves a higher Conv-KNRM and BLEU score when trained on more <Ad, query> data. It demonstrates that our TRIDENT can generate more relevant bidwords when more <Ad, query> data are used. This makes sense because more data could provide stronger supervision on the bidword generation process, leading to more meaningful bidwords. Moreover, the Self-BLEU of our model gets lower with the increase of <Ad, query> data size. One explanation is that more <Ad,

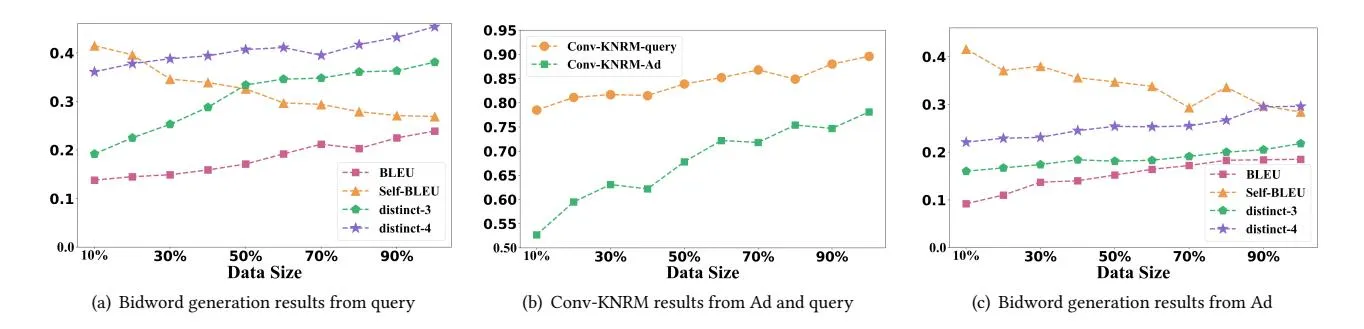
Figure 3: Performance curve of TRIDENT-A with different size of <A, Q> data

Models		Relevance		Diversity
		Conv-KNRM	BLEU	Self-BLEU	distinct-3	distinct-4
Transformer_base	Beam Search	0.800	0.175	0.639	0.135	0.211
	Constrained Beam Search	0.783	0.186	0.404	0.258	0.387
TRIDENT-A	Beam Search	0.784	0.228	0.518	0.270	0.346
	Constrained Beam Search	0.896	0.239	0.269	0.381	0.454

Table 5: Results of constrained beam search against beam search.

Model	Precision	Recall	F1-score
Transformer_base	0.156	0.075	0.101
TRIDENT-A	0.214	0.115	0.150

Table 6: Evaluation on online real data.

query> data can offer guide information to more training samples of bidwords.

4.6.2 Effect of the Constrained Beam Search. To clearly show the effect of the proposed constrained beam search, we examine the model performance using constrained beam search against the original beam search [33]. The results are reported in Table 5. As we can see, the Self-BLEU of constrained beam search are much lower than that of original beam search for both Transformer_base and TRIDENT-A. It demonstrates that the proposed constrained beam search can promote diversity in the generated candidates due to the fact that different head words could boost more diverse sentences [24]

4.7 Evaluation on Online Real Data

We additionally simulate an online experiment to examine whether the generated bidwords can be correctly recommended to relevant products in a real world e-commerce search engine. Specifically, we collect three pairs of data among A, Q and B from January 1 to July 15, 2020, of which the data before and after July 1 are split into training and test set, respectively. Taking <Q, B> pair as an example, we compute the precision, recall and F1-score between the generated bidwords and the golden ones for each query. The results are reported in Table 6, which shows the F1-score of our model is higher than that of Transformer_base. Therefore, we can

draw the conclusion that the bidwords generated by our model are more popular with advertisers, which will help to recall more related products.

4.8 Case Study

To gain an insight on how well the bidwords are generated through the proposed triangular architecture, we provide some examples. We randomly sample one Ad and one query as distinct sources, and collect the generated top-5 bidwords from all models.

The results are reported in Table 7, from which we can see that the bidwords generated by our TRIDENT are more relevant with the given Ad or query than other models. For example, given a query “翡翠手镯(Jade bracelet)”, other models may generate some irrelevant bidwords, such as “鉴定(Identification)” and “直播(Live broadcast)”, while those generated by our TRIDENT-A are all pointful and have different meanings. Above all, the proposed TRIDENT is capable of generating better bidwords in both relevance and diversity.

5 RELATED WORK

5.1 Bidword Generation

A lot of models have been proposed for bidword generation, since bidwords take an important part in sponsored search. Previous works are mostly retrieval based methods. Joshi and Motwani [19] construct a graph model to generate relevant bidwords from queries based on their similarity scores. Abhishek and Hosanagar [1] further establish a kernel function to improve the calculation of similarity scores. Fuxman et al. [14] propose to random walk with absorbing states for bidword generation. Chen et al. [5] propose a bidword suggestion method that exploits the semantic knowledge among concept hierarchy to find bidwords through the shared concepts.

Ad/Query	Max Pooling Method	Transformer_base	MT-A2B/Attn-Q2B	TRIDENT-A
	今日股票行情	股票行情分析	股票软件	今日股市行情
	(Today’s stock market)	(Stock market analysis)	(Stock software)	(Today’s stock market)
	股价	个股分析	股价	石油股价
股市行情怎样?	(Share price)	(Stock analysis)	(Share price)	(Oil stock price)
立马下载APP了解!	精股	走势图	股市行情	炒股
How is the stock market?	(Featured stocks)	(Tendency photos)	(Stock market)	(Trading stocks)
Download the APP right	分析	科技股	大盘	低价股
now to follow it!	(Analysis)	(Technology stocks)	(Market)	(Low-priced stocks)
	消息	利好消息	交流软件	科技股
	(News)	(Good news)	(Communication software)	(Technology stocks)
	手镯翡翠	翡翠手镯价格	玉镯	极品翡翠手镯
	(Jade bracelet)	(Price of Jade bracelet)	(Jade bracelet)	(The best Jade bracelet)
	玉镯	鉴定	冰种翡翠手镯	珠宝翡翠
翡翠手镯	(Jade bracelet)	(Identification)	(Ice Jadeite bracelet)	(Jewelry and jade)
(Jade bracelet)	玉手镯	买翡翠手镯	镯子	天然翡翠手镯
	(Jade bracelet)	(Buy jade bracelet)	(Bracelet)	(Natural jade bracelet)
	购买翡翠手镯	天然翡翠手镯	玉石	帝王绿翡翠
	(Buy jade bracelet)	(Natural jade bracelet)	(Jade)	(Emperor green jade)
	天然翡翠手镯	好的翡翠手镯	直播	玉手镯
	(Natural jade bracelet)	(Good jade bracelet)	(Live broadcast)	(Jade bracelet)

Table 7: Case study for the proposed TRIDENT. The top-5 bidwords are generated for each example. Sentence in the parentheses is the corresponding translation.

More recently, deep learning based methods have been applied for bidword recommendation with various neural network structures. Grbovic et al. [16] apply three language models to learn distributed query representations to promote query expansion. Lian et al. [26] directly employ the neural machine translation framework to generate bidwords from queries. Zhou et al. [48] use a reinforcement learning algorithm to generate domain constrained bidwords. Du et al. [9] predict the CTR between query and bidword using an attention model. Zhang et al. [45] apply a multi-task learning framework to imporve the semantic similarity between advertising and bidword.

All the above methods generate bidwords directly from Ad or query (say Ad bidword suggestion or query expansion), while our model exploits a triangular architecture to generate bidwords from both Ad and query.

5.2 Multilingual Neural Machine Translation

Multilingual training of Neural Machine Translation (NMT) has brought impressive accuracy improvements on low resource languages [27]. Dong et al. [8] extend the single NMT to a multi-task learning framework that shares source language representation and separates the modeling of different target language translation. Zoph et al. [50] propose a transfer learning method to improve the performance of low-resource language pairs. Firat et al. [11] enable a single neural translation model for each language pair and all the language pairs share a single attention mechanism. A TA-NMT model is exploited in [34] to improve the performance of the low resource pair by constructing a triangular architecture.

To the best of our knowledge, this is the first work exploiting a triangular framework to generate more relevant and diverse bidwords with the help of the high-quality <Ad, query> data.

5.3 Neural Text Generation

Recently generative neural networks have been proven to be quite successful in structured prediction tasks such as machine translation [47], bidword generation [26] and query expansion [23].

Sutskever et al. [41] propose a sequence-to-sequence (Seq2Seq) framework for machine translation. Bahdanau et al. [3] then extend the Seq2Seq framework with an attention mechanism. Seq2Seq framework has also been used in many natural language generation tasks, such as abstractive summarization [35] and dialog generation [38, 40]. However, neural generative models employing the Seq2Seq framework tend to produce generic and meaningless outputs [25]. To address this problem, Miao et al. propose CGMH [29], a constrained generation method using Metropolis-Hastings sampling to improve sentence generation quality. Further, a novel objective function based on maximizing mutual information is proposed by Li et al. [24] to generate more meaningful dialogue responses. Song et al. employs adversarial training to improve both the quality and diversity of generated texts [39]. Recently, the Transformer encoder-decoder framework [42] is also employed in text generation models [43] to boost coherence.

6 CONCLUSION

Sponsored search auction is also called bidword auction, which is an indispensable part of commercial search engine. Generating relevant and diverse bidwords for search queries and advertisements are crucial and can bring great revenues in sponsored search. However, directly employing the Seq2Seq model in bidword generation does not yield satisfactory results, due to the fact that the Seq2Seq model is data-driven and heavily relies on the training data, while the training data of <query/advertisement, bidword> may be noisy because of the keyword bidding problem. In this paper, we propose a Triangular Bidword Generation Model (TRIDENT), which exploits

the high-quality <query, advertisement> data as a supervision signal to indirectly guide the bidword generation process through a triangle training framework. Experimental results show that our proposed TRIDENT can generate relevant and diverse bidwords for both queries and advertisements, which are more popular with advertisers.

REFERENCES

• [1] Vibhanshu Abhishek and Kartik Hosanagar. 2007. Keyword generation for search engine advertising using semantic similarity between terms. In Proceedings of the ninth international conference on Electronic commerce. ACM, 89–94.

• [2] Gagan Aggarwal, Ashish Goel, and Rajeev Motwani. 2006. Truthful auctions for pricing search keywords. In Proceedings of the 7th ACM conference on Electronic commerce. ACM, 1–7.

• [3] Dzmitry Bahdanau, Kyunghyun Cho, and Yoshua Bengio. 2014. Neural machine translation by jointly learning to align and translate. In ICLR.

• [4] Pi-Chuan Chang, Michel Galley, and Christopher D Manning. 2008. Optimizing Chinese word segmentation for machine translation performance. In Proceedings of the third workshop on statistical machine translation. 224–232.

• [5] Yifan Chen, Gui-Rong Xue, and Yong Yu. 2008. Advertising keyword suggestion based on concept hierarchy. In Proceedings of the 2008 WSDM. ACM, 251–260.

• [6] Kyunghyun Cho, Bart Merrienboer, Caglar Gulcehre, Fethi Bougares, Holger Schwenk, and Yoshua Bengio. 2014. Learning Phrase Representations using RNN Encoder-Decoder for Statistical Machine Translation. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing.

• [7] Zhuyun Dai, Chenyan Xiong, Jamie Callan, and Zhiyuan Liu. 2018. Convolutional neural networks for soft-matching n-grams in ad-hoc search. In Proceedings of the eleventh ACM international conference on web search and data mining. 126–134.

• [8] Daxiang Dong, Hua Wu, Wei He, Dianhai Yu, and Haifeng Wang. 2015. Multitask learning for multiple language translation. In Proceedings of the 53rd Annual Meeting of the Association for Computational Linguistics and the 7th International Joint Conference on Natural Language Processing. 1723–1732.

• [9] Nan Du, Yaliang Li, and Wei Fan. 2018. Systems and methods for an attentionbased framework for click through rate (ctr) estimation between query and bidwords. US Patent App. 15/206,966.

• [10] Eyal Even Dar, Vahab S Mirrokni, Shanmugavelayutham Muthukrishnan, Yishay Mansour, and Uri Nadav. 2009. Bid optimization for broad match ad auctions. In Proceedings of the 18th international conference on World wide web. 231–240.

• [11] Orhan Firat, Kyunghyun Cho, and Yoshua Bengio. 2016. Multi-Way, Multilingual Neural Machine Translation with a Shared Attention Mechanism. In Proceedings of the 2016 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies. 866–875.

• [12] Orhan Firat, Kyunghyun Cho, Baskaran Sankaran, Fatos T Yarman Vural, and Yoshua Bengio. 2017. Multi-way, multilingual neural machine translation. Computer Speech & Language 45 (2017), 236–252.

• [13] Joseph L Fleiss and Jacob Cohen. 1973. The equivalence of weighted kappa and the intraclass correlation coefficient as measures of reliability. Educational and psychological measurement 33, 3 (1973), 613–619.

• [14] Ariel Fuxman, Panayiotis Tsaparas, Kannan Achan, and Rakesh Agrawal. 2008. Using the wisdom of the crowds for keyword generation. In Proceedings of the 17th international conference on World Wide Web. ACM, 61–70.

• [15] David G Garber and Adam M Feldstein. 2004. Flexible keyword searching. US Patent 6,748,387.

• [16] Mihajlo Grbovic, Nemanja Djuric, Vladan Radosavljevic, Fabrizio Silvestri, and Narayan Bhamidipati. 2015. Context-and Content-aware Embeddings for Query Rewriting in Sponsored Search. (2015).

• [17] Stefano M Iacus, Gary King, and Giuseppe Porro. 2012. Causal inference without balance checking: Coarsened exact matching. Political analysis 20, 1 (2012), 1–24.

• [18] Eric Jang, Shixiang Gu, and Ben Poole. 2017. CATEGORICAL REPARAMETERI-ZATION WITH GUMBEL-SOFTMAX. stat 1050 (2017), 5.

• [19] Amruta Joshi and Rajeev Motwani. 2006. Keyword Generation for Search Engine Advertising. In Proceedings of the Sixth IEEE International Conference on Data Mining-Workshops. IEEE Computer Society, 490–496.

• [20] Leslie Pack Kaelbling, Michael L Littman, and Andrew W Moore. 1996. Reinforcement learning: A survey. Journal of artificial intelligence research 4 (1996).

• [21] Diederik P Kingma and Jimmy Ba. 2014. Adam: A method for stochastic optimization. (2014).

• [22] Tomáš Kočisky, Gábor Melis, Edward Grefenstette, Chris Dyer, Wang Ling, ` Phil Blunsom, and Karl Moritz Hermann. 2016. Semantic Parsing with Semi-Supervised Sequential Autoencoders. In Proceedings of the 2016 Conference on Empirical Methods in Natural Language Processing. 1078–1087.

• [23] Mu-Chu Lee, Bin Gao, and Ruofei Zhang. 2018. Rare query expansion through generative adversarial networks in search advertising. In Proceedings of the 24th KDD. ACM, 500–508.

• [24] Jiwei Li, Michel Galley, Chris Brockett, Jianfeng Gao, and Bill Dolan. 2016. A Diversity-Promoting Objective Function for Neural Conversation Models. In Proceedings of the 2016 NAACL. 110–119.

• [25] Jiwei Li, Will Monroe, and Dan Jurafsky. 2016. A simple, fast diverse decoding algorithm for neural generation. arXiv preprint arXiv:1611.08562 (2016).

• [26] Yijiang Lian, Zhijie Chen, Jinlong Hu, Kefeng Zhang, Chunwei Yan, Muchenxuan Tong, Wenying Han, Hanju Guan, Ying Li, Ying Cao, et al. 2019. An end-to-end Generative Retrieval Method for Sponsored Search Engine–Decoding Efficiently into a Closed Target Domain. arXiv preprint arXiv:1902.00592 (2019).

• [27] Zehui Lin, Xiao Pan, Mingxuan Wang, Xipeng Qiu, Jiangtao Feng, Hao Zhou, and Lei Li. 2020. Pre-training Multilingual Neural Machine Translation by Leveraging Alignment Information. In Proceedings of the 2020 (EMNLP). 2649–2663.

• [28] Miaofeng Liu, Jialong Han, Haisong Zhang, and Yan Song. 2018. Domain Adaptation for Disease Phrase Matching with Adversarial Networks. In Proceedings of the BioNLP 2018 workshop. 137–141.

• [29] Ning Miao, Hao Zhou, Lili Mou, Rui Yan, and Lei Li. 2019. Cgmh: Constrained sentence generation by metropolis-hastings sampling. In Proceedings of the AAAI Conference on Artificial Intelligence, Vol. 33. 6834–6842.

• [30] Kishore Papineni, Salim Roukos, Todd Ward, and Wei-Jing Zhu. 2002. BLEU: a method for automatic evaluation of machine translation. In Proceedings of the 40th Annual Meeting of the Association for Computational Linguistics. Association for Computational Linguistics, 311–318.

• [31] Jeffrey Pennington, Richard Socher, and Christopher D Manning. 2014. Glove: Global vectors for word representation. In Proceedings of the 2014 conference on empirical methods in natural language processing (EMNLP). 1532–1543.

• [32] Anand Rajaraman and Jeffrey David Ullman. 2011. Mining of massive datasets. Cambridge University Press.

• [33] D Raj Reddy et al. 1977. Speech Understanding Systems: A Summary of Results of the Five-Year Research Effort. Department of Computer Science.

• [34] Shuo Ren, Wenhu Chen, Shujie Liu, Mu Li, Ming Zhou, and Shuai Ma. 2018. Triangular Architecture for Rare Language Translation. In ACL 2018. 56–65.

• [35] Alexander M Rush, Sumit Chopra, and Jason Weston. 2015. A Neural Attention Model for Abstractive Sentence Summarization. In Proceedings of the 2015 Conference on Empirical Methods in Natural Language Processing. 379–389.

• [36] Rico Sennrich, Barry Haddow, and Alexandra Birch. 2015. Neural machine translation of rare words with subword units. (2015).

• [37] Xiaoyu Shen, Hui Su, Wenjie Li, and Dietrich Klakow. 2018. NEXUS Network: Connecting the Preceding and the Following in Dialogue Generation. In EMNLP 2018. 4316–4327.

• [38] Wenxian Shi, Hao Zhou, Ning Miao, and Lei Li. 2020. Dispersed Exponential Family Mixture VAEs for Interpretable Text Generation. In International Conference on Machine Learning. PMLR, 8840–8851.

• [39] Yuxuan Song, Ning Miao, Hao Zhou, Lantao Yu, Mingxuan Wang, and Lei Li. 2020. Improving Maximum Likelihood Training for Text Generation with Density Ratio Estimation. In International Conference on Artificial Intelligence and Statistics. PMLR, 122–132.

• [40] Zhenqiao Song, Xiaoqing Zheng, Lu Liu, Mu Xu, and Xuan-Jing Huang. 2019. Generating responses with a specific emotion in dialog. In Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics. 3685–3695.

• [41] Ilya Sutskever, Oriol Vinyals, and Quoc V Le. 2014. Sequence to sequence learning with neural networks. In Advances in neural information processing systems.

• [42] Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N Gomez, Łukasz Kaiser, and Illia Polosukhin. 2017. Attention is all you need. In Advances in neural information processing systems. 5998–6008.

• [43] Vladimir Vlasov, Johannes EM Mosig, and Alan Nichol. 2019. Dialogue transformers. arXiv preprint arXiv:1910.00486 (2019).

• [44] Haibing Wu and Xiaodong Gu. 2015. Max-pooling dropout for regularization of convolutional neural networks. In International Conference on Neural Information Processing. Springer, 46–54.

• [45] Hongchun Zhang, Tianyi Wang, Xiaonan Meng, Yi Hu, and Hao Wang. 2019. Improving Semantic Matching via Multi-Task Learning in E-Commerce.. In eCOM@ SIGIR.

• [46] Zhichen Zhao, Huimin Ma, and Xiaozhi Chen. 2014. Protected Pooling Method of Sparse Coding in Visual Classification. In Computer Vision and Graphics, Leszek J. Chmielewski, Ryszard Kozera, Bok-Suk Shin, and Konrad Wojciechowski (Eds.). Springer International Publishing, Cham, 680–687.

• [47] Zaixiang Zheng, Hao Zhou, Shujian Huang, Lei Li, Xin-Yu Dai, and Jiajun Chen. 2019. Mirror-Generative Neural Machine Translation. In ICLR.

• [48] Hao Zhou, Minlie Huang, Yishun Mao, Changlei Zhu, Peng Shu, and Xiaoyan Zhu. 2019. Domain-Constrained Advertising Keyword Generation. In The World Wide Web Conference. ACM, 2448–2459.

• [49] Yaoming Zhu, Sidi Lu, Lei Zheng, Jiaxian Guo, Weinan Zhang, Jun Wang, and Yong Yu. 2018. Texygen: A benchmarking platform for text generation models. In The 41st International ACM SIGIR Conference on Research & Development in Information Retrieval. ACM, 1097–1100.

• [50] Barret Zoph, Deniz Yuret, Jonathan May, and Kevin Knight. 2016. Transfer Learning for Low-Resource Neural Machine Translation. In EMNLP 2016.